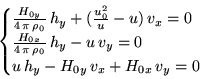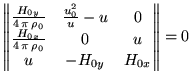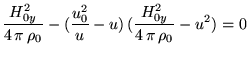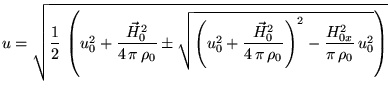

След.: Другой подход к получению
Выше: Магнитогидродинамические волны.
Пред.: Альвеновские волны.
Теперь выберем из уравнений (26), (27) тройку
уравнений, содержащую 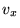 ,
, 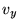 и
и 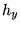 . Получим систему
. Получим систему
Мы опять имеем систему линейных уравнений, причем опять, так как количество
независимых переменных равно количеству уравнений,
то для существования ненулевых решений нам надо приравнять
нулю детерминант системы.
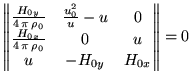 |
(34) |
Расписывая очевидным образом определитель по первой строке, будем иметь
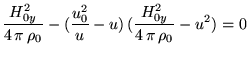 |
(35) |
Домножая на 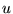 и приводя подобные члены (c учетом
и приводя подобные члены (c учетом
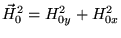 ),
получим:
),
получим:
Очевидным образом, решая это биквадратное уравнение, получим
(учтя, что отрицательные значения 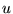 брать не имеет
смысла):
брать не имеет
смысла):
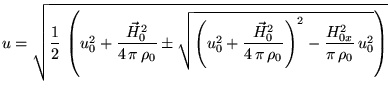 |
(37) |
Так как, нетрудно видеть, в последнем равенстве, независимо от
выбора знака плюс-минуса получается вещественное значение
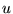 . Следовательно мы будем иметь 2 типа данных волн - так называемая
медленная магнитозвуковая (выбор знака минус) и быстрая магнитозвуковая
(выбор знака плюс). Название этих волн происходит от того, что,
если рассмотреть приближение слабого
поля
. Следовательно мы будем иметь 2 типа данных волн - так называемая
медленная магнитозвуковая (выбор знака минус) и быстрая магнитозвуковая
(выбор знака плюс). Название этих волн происходит от того, что,
если рассмотреть приближение слабого
поля
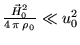 , то для быстрой волны
, то для быстрой волны
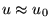 и, как видно из системы (33),
и, как видно из системы (33),
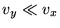 , т.е.
мы будем иметь обычную звуковую волну.
, т.е.
мы будем иметь обычную звуковую волну.
root
2003-04-25