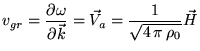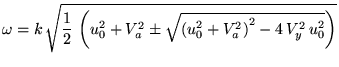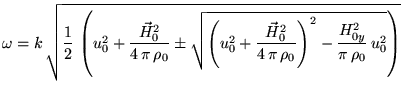

След.: Об этом документе ...
Выше: Магнитогидродинамические волны.
Пред.: Магнитозвуковые волны.
В начале мы будем исходить из общих уравнений для полей в сплошной
движущейся среде. Хотя потом мы будем использовать в частности приближение
идеально проводящей жидкости. Соответственно общие уравнения для полей в
движущейся среде в нерелятивистком приближении будут выглядеть следующим
образом (вывод в лекциях).
Также,напоминая, используя уравнение непрерывности, из уравнения (40)
можно получить другое просто полезное уравнение:
Наконец, можно написать выражение для величины объемной силы действующей на
жидкость - это сила Лоренца. Собственно, так как объемных зарядов нет, то
объемная сила
![$\displaystyle \vec{f}=\frac{1}{c}[\vec{j} \vec{H}]$](img83.png) |
(42) |
Соотвественно так как
![$\displaystyle j=\sigma \vec{E'}=\sigma (\vec{E}+\frac{1}{c}[\vec{v} \vec{H}])$](img84.png) |
(43) |
подставляя 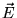 из уравнения (39) получим, что
из уравнения (39) получим, что
![$\displaystyle \vec{f}=-\frac{1}{4 \pi}[\vec{H} rot \vec{H}]$](img86.png) |
(44) |
Теперь немного снова об уравнениях гидродинамики. Если рассматривать не
идеальную жидкость, а жидкость с вязкостью, то мы будем иметь не уравнение
Эйлера, а уравнение Навье-Стокса. Напомним откуда оно собственно берется:
При введении в рассмотрение вязких сил тензор натяжений перестает быть
диагональным, и к тензору натяжений, в первом приближении, добавляются члены
линейные по градиенту скорости, и соотвественно учитывая симметричность
этого тензора оказывается, что общий вид вязкого тензора напряжений зависит
от двух констант, т. н. первой и второй вязкостей.
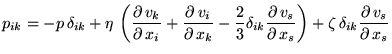 |
(45) |
Для такого тензора напряжений вместо уравнения Эйлера получается соотвественно
следующее уравнение (Навье-Стокса):
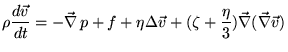 |
(46) |
Для рассмотрения магнитогидродинамической волны в жидкости нам
надо рассмотреть малые добавки к стационарным значениям
параметров в жидкости, таких как H, 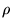 ,
, 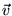 , p.
, p.
Причем мы будем
рассматривать волны в жидкости при условии отсутствия макроскопических
потоков в жидкости. Таким образом стационарное значение значение
скорости принято равным нулю
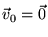 . Для других
параметров условие малости возмущений запишется следующим образом
. Для других
параметров условие малости возмущений запишется следующим образом
Макроскопически магнитное поле будем считать однородным, жидкость
однородной.
Для получения уравнений распространения возмущений в среде нам очевидно
должно понадобится уравнение состояния, вообще говоря выглядящее вот так
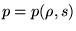 , где s - энтропия.
, где s - энтропия.
Дальше, можно собственно, либо сказать,
что рассматриваем например адиабатический процесс и тогда
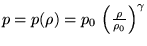 . Можно же сказать,
что так как мы рассматриваем малые возмущения, то учитывая то, что
. Можно же сказать,
что так как мы рассматриваем малые возмущения, то учитывая то, что
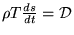 , где
, где
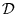 - диссипативная
функция, которая квадратична по скоростям - т.е. в нашем приближении ей
можно пренебречь, а следовательно считать s постоянной, и таким образом
иметь опять же уравнение состояния в виде
- диссипативная
функция, которая квадратична по скоростям - т.е. в нашем приближении ей
можно пренебречь, а следовательно считать s постоянной, и таким образом
иметь опять же уравнение состояния в виде 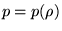 Учитывая то, что мы имеем уравнение состояния
Учитывая то, что мы имеем уравнение состояния 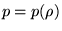 , то раскладывая
получим:
, то раскладывая
получим:
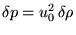 |
|
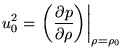 |
(49) |
где через 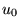 обозначена скорость звука в жидкости.
Теперь, для дальнейших вычислений заменим субстанциональные производные на
эйлеровы производные. Дело в том ,что, как известно, субстанциональная
производная выражается через Эйлерову производную следующим образом:
обозначена скорость звука в жидкости.
Теперь, для дальнейших вычислений заменим субстанциональные производные на
эйлеровы производные. Дело в том ,что, как известно, субстанциональная
производная выражается через Эйлерову производную следующим образом:
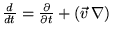 . А в предположении малых возмущении мы просто
получаем равенство субстанциональной и Эйлеровой производных.
Наконец напишем несколько очевидных равенств верных с точностью до
бесконечно малых более высокого порядка
. А в предположении малых возмущении мы просто
получаем равенство субстанциональной и Эйлеровой производных.
Наконец напишем несколько очевидных равенств верных с точностью до
бесконечно малых более высокого порядка
![$\displaystyle [\vec{H} rot \vec{H}]=[H_0 rot \vec{\delta H}]$](img99.png) |
|
![$\displaystyle [\vec{v}\vec{H}]=[\vec{\delta v} \vec{H_0}]$](img100.png) |
(50) |
Соответственно, тогда основные уравнения запишутся следующим образом:
Наша задача сейчас - получить волновое уравнение для возмущений в жидкости.
Если такое волновое уравнение будет получено, то это будет автоматически
означать существование волн. Однако получить его в самом общем виде сложно,
если вообще возможно. Поэтому оно будет получено собственно для плоских
волн. Но для начала преобразуем уравнения (51)- (53). Как
всегда бывает, для получения волнового уравнения надо к одному уравнению
применить дифференциальный оператор по координатам, а другое уравнение
продифференцировать по времени. Так и сделаем. Уравнение (51)
продифференцируем по времени, а к уравнению (53) применим оператор
градиента и после этого подставим в продифференцированное (51) и
поделим на 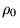 .
Тогда получим:
.
Тогда получим:
Теперь собственно рассмотрим плоские волны:
Здесь,
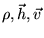 - постоянные
величины , являющиеся амплитудами соответствующих колебаний.
Теперь, учитывая то, что
- постоянные
величины , являющиеся амплитудами соответствующих колебаний.
Теперь, учитывая то, что
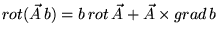 |
|
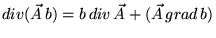 |
(57) |
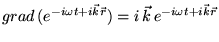 |
|
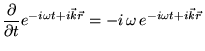 |
(58) |
уравнение (55) преобразуется в
Чтобы получить волновое уравнение нам надо избавиться в последнем уравнении
от еще одной независимой переменной и оставить только скорость. Для этого
подставляя уравнения (56) в уравнение (52). Тогда
получим:
Далее, подставим последнее выражение в (59), обозначив при этом
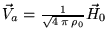 (по размерности это
скорость) получим, приводя
подобные члены:
(по размерности это
скорость) получим, приводя
подобные члены:
![$\displaystyle -\omega^2\left(1+\frac{i \eta}{\omega \rho_0}\vec{k}^2\right)\v...
...left[\vec{k}\left[\vec{k}\left[\vec{v} \vec{V}_a\right]\right]\right]\right]=0$](img112.png) |
(61) |
Так собственно мы получили собственно фактически волновое уравнение для
скорости в достаточно общих предположениях (малые возмущения в вязкой,
неидеально проводящей жидкости в однородном магнитном поле).
Получим также несколько вспомогательных уравнений. Подставляя
(56) в (53) получим:
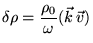 |
(62) |
Подставляя же (56) и (60) в (54) получим:
![$\displaystyle \vec{E}=-\frac{1}{c}[\vec{v} \vec{H}_0]-\frac{i c}{4 \pi \sig...
...ega}} \left[\vec{k}\left[\vec{k}\left[\vec{v} \vec{H}_0\right]\right]\right]$](img114.png) |
(63) |
Теперь же наконец можно все-таки перейти к тем приближениям, о которых
говорилось до этого: т. е. приближения идеальной и идеально проводящей
жидкости. Эти приближения естественно сводятся к следующему:
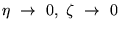 и
и
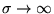 Тогда наш основной набор уравнений будет выглядеть следующим образом:
Тогда наш основной набор уравнений будет выглядеть следующим образом:
Раскроем векторное произведение
Тогда уравнение (64) запишется следующим образом:
И называется это уравнение Основным спектральным уравнением.
Теперь перейдем собственно к его решению. Очевидно, так как уравнение
векторное, то мы имеем на самом деле однородную линейную систему из трех
уравнений, которая имеет решение только при некотором условиях на
коэффициенты (эти условия на самом деле будут дисперсионными уравнениями для
соответствующих волн (т.е. соотношениями между волновым вектором и частотой)).
Распишем для получения этих условий уравнение (68) по осям.
Причем для этого ориентируем систему координат так, чтобы
вектор 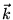 был направлен вдоль оси Y, а вектор
был направлен вдоль оси Y, а вектор 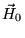 лежал в
плоскости YZ (очевидно, что мы всегда можем так выбрать систему координат).
Итак тогда:
лежал в
плоскости YZ (очевидно, что мы всегда можем так выбрать систему координат).
Итак тогда:
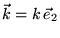 |
|
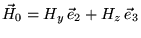 |
(69) |
Итак, уравнение (68) запишется:
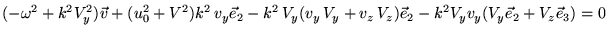 |
(70) |
Распишем последнее уравнение по координатам:
Видно что в системе уравнения делятся, т.е. есть уравнение содержащее только
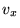 , а другая пара уравнений содержит
, а другая пара уравнений содержит 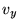 с
с 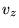 . Это значит на самом
деле,что в жидкости могут распространяться независимо!!! друг от друга два
типа возмущений.
Рассмотрим первый тип возмущений, происходящий из первого уравнения системы.
Он соответствует
. Это значит на самом
деле,что в жидкости могут распространяться независимо!!! друг от друга два
типа возмущений.
Рассмотрим первый тип возмущений, происходящий из первого уравнения системы.
Он соответствует 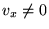 . Для этого типа волн (называемых
Альвеновскими) мы получаем дисперсионное уравнение:
. Для этого типа волн (называемых
Альвеновскими) мы получаем дисперсионное уравнение:
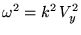 |
(72) |
или более общо:
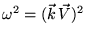 |
(73) |
А отсюда
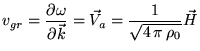 |
|
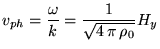 |
(74) |
Как нетрудно видеть теперь мы получили поперечную волну, причем изменений
плотности в ней нет и она следовательно возможна как в сжимаемой так и в
несжимаемой жидкости. Энергия в этой волне ( в соответствии с направлением
групповой скорости) распространяется вдоль магнитного поля.
Рассмотрим теперь последние два уравнения из (71) Опять же
распишем условие существования нетривиального решения у двух линейных
уравнений - равенство нулю определителя. Получится следующее уравнение:
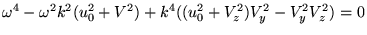 |
(75) |
Решая это биквадратное уравнение, получим:
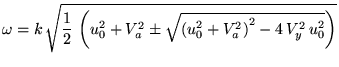 |
(76) |
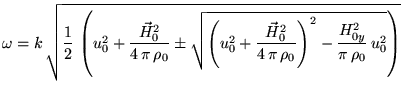 |
(77) |
Эти волны уже не являются ни чисто продольными, ни чисто поперечными, хотя и
называются магнитозвуковыми (медленной магнитозвуковой ,если в последней
формуле выбран знак минус, и быстрой, если наоборот). Называются они
магнитозвуковыми, так как в приближении слабого магнитного поля
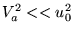 видно что скорость быстрой магнитозвуковой волны будет
равна скорости звука, и из уравнения (68) видно, что волна
получится продольная.
видно что скорость быстрой магнитозвуковой волны будет
равна скорости звука, и из уравнения (68) видно, что волна
получится продольная.


След.: Об этом документе ...
Выше: Магнитогидродинамические волны.
Пред.: Магнитозвуковые волны.
root
2003-04-25
![$\displaystyle \frac{\partial{\vec{H}}}{\partial t}=rot [\vec{v} \vec{H}]+\frac{c^2}{4\pi\sigma}\Delta\vec{H}$](img81.png)
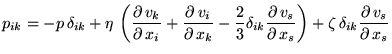
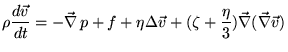
![]() . Можно же сказать,
что так как мы рассматриваем малые возмущения, то учитывая то, что
. Можно же сказать,
что так как мы рассматриваем малые возмущения, то учитывая то, что
![]() , где
, где
![]() - диссипативная
функция, которая квадратична по скоростям - т.е. в нашем приближении ей
можно пренебречь, а следовательно считать s постоянной, и таким образом
иметь опять же уравнение состояния в виде
- диссипативная
функция, которая квадратична по скоростям - т.е. в нашем приближении ей
можно пренебречь, а следовательно считать s постоянной, и таким образом
иметь опять же уравнение состояния в виде ![]() Учитывая то, что мы имеем уравнение состояния
Учитывая то, что мы имеем уравнение состояния ![]() , то раскладывая
получим:
, то раскладывая
получим:
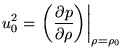
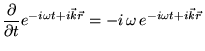
![$\displaystyle -\omega^2\left(1+\frac{i \eta}{\omega \rho_0}\vec{k}^2\right)\v...
...left[\vec{k}\left[\vec{k}\left[\vec{v} \vec{V}_a\right]\right]\right]\right]=0$](img112.png)
![$\displaystyle \vec{E}=-\frac{1}{c}[\vec{v} \vec{H}_0]-\frac{i c}{4 \pi \sig...
...ega}} \left[\vec{k}\left[\vec{k}\left[\vec{v} \vec{H}_0\right]\right]\right]$](img114.png)