

След.: Альвеновские волны.
Выше: Магнитогидродинамические волны.
Пред.: Общие уравнения для малых
Систему уравнений (11) - (14) нам и необходимо
решить для того, чтобы рассмотреть магнитогидродинамические волны.
Естественно решать мы ее будем в упрощенном виде, а именно
рассматривая плоские монохроматические волны.
Здесь,
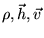 - постоянные
величины , являющиеся амплитудами соответствующих колебаний.
Теперь, учитывая то, что
- постоянные
величины , являющиеся амплитудами соответствующих колебаний.
Теперь, учитывая то, что
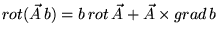 |
|
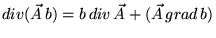 |
(16) |
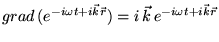 |
|
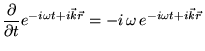 |
(17) |
и подстановку (15) система уравнений
(11) - (14), соотвественно,преобразуется
в линейную систему для амплитуд волн плотности, магнитного
поля и скорости:
Наконец, подставляя 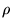 из
(18) в уравнение (19), а также учтя то, что уравнение
(20) есть следствие уравнения (21)
(из (21) следует, что
из
(18) в уравнение (19), а также учтя то, что уравнение
(20) есть следствие уравнения (21)
(из (21) следует, что 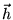 ортогонально
ортогонально
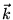 , а следовательно
, а следовательно
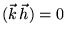 ) получаем 2 линейных
уравнения относительно
) получаем 2 линейных
уравнения относительно 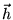 и
и
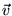 :
:
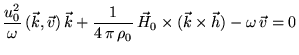 |
(22) |
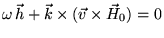 |
(23) |
Теперь, положим
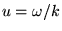 (впоследствии эта величина очевидно окажется фазовой скоростью получившейся волны).
Направим
(впоследствии эта величина очевидно окажется фазовой скоростью получившейся волны).
Направим 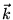 вдоль оси
Х. А вектор
вдоль оси
Х. А вектор 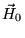 , расположим в плоскости ХУ (очевидно, что
всегда так можем повернуть систему координат).
Распишем также векторные произведения:
, расположим в плоскости ХУ (очевидно, что
всегда так можем повернуть систему координат).
Распишем также векторные произведения:
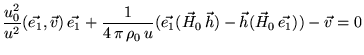 |
(24) |
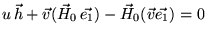 |
(25) |
Тогда последние два
уравнения можно расписать в координатах (учитывая, что 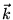 имеет
ненулевую X компоненту,
имеет
ненулевую X компоненту, 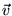 - Y,Z компоненты,
- Y,Z компоненты,
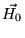 - X,Y компоненты, а
- X,Y компоненты, а 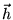 - Y,Z
компоненты (из (20)):
- Y,Z
компоненты (из (20)):
Как легко видеть среди последних пяти уравнений есть два уравнения содержащие
только Z-овые проекции векторов 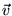 и
и 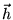 и
есть три уравнения содержащие только Y-овые проекции
и
есть три уравнения содержащие только Y-овые проекции 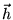 и X-овые и Y-овые проекции
и X-овые и Y-овые проекции 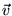 . Эти две
группы уравнений независимы, таким образом можно утверждать, о
том, что 2 различных типа волн (проходящих в проводящей жидкости
независимо друг от друга). Итак рассмотрим эти 2 типа волн.
. Эти две
группы уравнений независимы, таким образом можно утверждать, о
том, что 2 различных типа волн (проходящих в проводящей жидкости
независимо друг от друга). Итак рассмотрим эти 2 типа волн.


След.: Альвеновские волны.
Выше: Магнитогидродинамические волны.
Пред.: Общие уравнения для малых
root
2003-04-25
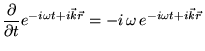
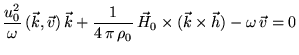
![]() (впоследствии эта величина очевидно окажется фазовой скоростью получившейся волны).
Направим
(впоследствии эта величина очевидно окажется фазовой скоростью получившейся волны).
Направим ![]() вдоль оси
Х. А вектор
вдоль оси
Х. А вектор ![]() , расположим в плоскости ХУ (очевидно, что
всегда так можем повернуть систему координат).
Распишем также векторные произведения:
, расположим в плоскости ХУ (очевидно, что
всегда так можем повернуть систему координат).
Распишем также векторные произведения:
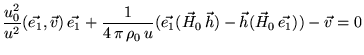
![]() имеет
ненулевую X компоненту,
имеет
ненулевую X компоненту, ![]() - Y,Z компоненты,
- Y,Z компоненты,
![]() - X,Y компоненты, а
- X,Y компоненты, а ![]() - Y,Z
компоненты (из (20)):
- Y,Z
компоненты (из (20)):
![]() и
и ![]() и
есть три уравнения содержащие только Y-овые проекции
и
есть три уравнения содержащие только Y-овые проекции ![]() и X-овые и Y-овые проекции
и X-овые и Y-овые проекции ![]() . Эти две
группы уравнений независимы, таким образом можно утверждать, о
том, что 2 различных типа волн (проходящих в проводящей жидкости
независимо друг от друга). Итак рассмотрим эти 2 типа волн.
. Эти две
группы уравнений независимы, таким образом можно утверждать, о
том, что 2 различных типа волн (проходящих в проводящей жидкости
независимо друг от друга). Итак рассмотрим эти 2 типа волн.