Возмущающий потенциал, гравитационные аномалии. Краевое условие для возмущающего потенциала. Внешние и внутренние краевые задачи Дирихле, Неймана, смешанные краевые задачи. Определение высот геоида методом Стокcа. Функция Стокса. Определение уклонений отвеса. Формулы Венинг-Мейнеса.
Среди специалистов по высей геодезии широко применяется термин возмущающий потенциал, как разность между реальным и нормальным потенциалами в одной точке. Нельзя сказать, что термин удачен. В небесной механике часто употребляется термин возмущающие силы, возмущающая силовая функция, возмущения. Возникает вопрос, что именно возмущает данная сила? Для небесной механики ответ ясен -- закон движения тела, делает его отличным от кеплеровского, невозмущенного. Правда, терминология московской и петербургской школ небесных механиков различаются. Москвичи говорят функция возмущающая, а петербуржцы -- пертурбационная. Так что же "возмущает" возмущающий потенциал? Ответ -- ничего. По-видимому прав австрийский геодезист Г.Мориц, который предлагает ввести термин аномалия потенциала. Говорим же мы аномалия силы тяжести, имея в виду разность реальной и нормальной силы тяжести! Но отдавая дань традиции, мы будем употреблять термин возмущающий потенциал именно как разность реального и нормального потенциалов тяжести или притяжения взятых в одной и той же точке.
Возьмем точку 
на поверхности геоида
-- уровенной поверхности -- с координатами 
, где 
геодезическая высота точки (расстояние от уровенной
поверхности до эллипсоида) Другими словами это
высота геоида в точке . Две другие координаты -- 
и 
соответственно
геодезические широта и долгота
(см. лекцию 2, раздел 2.3).
На поверхности эллипсоида
точку с такими же значениями широты и долготы будем обозначать буквой 
.
Понятно, что высота этой точки равна нулю. Сила тяжести в точке :
Нормальная сила тяжести в точке :
Разность абсолютных значений этих векторов определяет смешанную гравитационную аномалию.
Возмущающий потенциал в точке (на эллипсоиде) равен
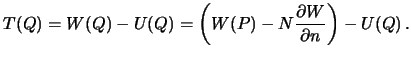
Однако, поскольку
, получим
Определим смешанную аномалию
В первом слагаемом мы дифференцируем потенциал по внешней нормали к геоиду,
а во втором -- к эллипсоиду. Эти два направления, вообще говоря, не
совпадают. Правда, отличие не велико и ошибка составляет всего
, то есть величину порядка квадрата отклонения
отвесной линии. Это
существенно меньше квадрата сжатия, поэтому в нашем приближении можно не
делать различия в направлениях отвесной линии и нормали к эллипсоиду.
"Опустим" значение силы тяжести из точки в точку , применяя формулы
линейного приближения
Вертикальный градиент силы тяжести, как мы видели (см. лекцию 7, уравнение (7.12)), зависит от радиусов кривизны нормальных сечений и угловой скорости вращения Земли
Пренебрегая малыми порядка 
, можно пренебречь и членом
. Кроме того, поскольку также малая величина
(сравнению с 
), можно не
учитывать различия между радиусами кривизны меридионального сечения и
сечения в первом вертикале. После упрощений, формула (8.3) принимает вид
Теперь смешанную аномалию можно записать так
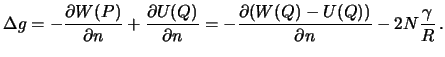
Разность 
есть возмущающий потенциал в точке , а тот, в свою
очередь, связан с высотой геоида формулой (8.1).
Заменяя в этой формуле
реальное значение силы тяжести на нормальное, получим
. Теперь
смешанную аномалию можно выразить через возмущающий потенциал следующим
образом
Итак, задача определения фигуры геоида (поверхности уровня относительно эллипсоида) сводится к определению гармонической функции Т -- возмущающего потенциала, который линейно связан с высотой геоида. Проблема интегрирования уравнения Лапласа, при условии, что на заданной поверхности искомая функция подчиняется некоторому условию, которое называют краевым условием, принадлежит к большому классу краевых задач, с некоторыми из них мы и познакомимся.
Попытаемся решить следующую задачу. Дано дифференциальное уравнение Лапласа,
определяющее функцию 
, гармоническую в некоторой области, ограниченной
замкнутой поверхностью 
. Все значения этой функции на границе области, то
есть на поверхности , известны. Из всех решений уравнения Лапласа
требуется выбрать только те, которые удовлетворяют краевому условию. Решение
этой задачи существенным образом зависит от вида граничной поверхности.
Покажем, как она решается, если заданная поверхность -- сфера. В данной
формулировке имеем дело с внутренней проблемой Дирихле.
Иногда требуется определить гармоническую функцию вне граничной поверхности. Тогда это внешняя проблема Дирихле.
Допустим, что искомая функция задана на поверхности сферы 
значениями
. Разложим функцию
в ряд Лапласа:
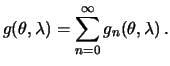
| Внутренняя проблема Дирихле | Внешняя проблема Дирихле |
| Искомым решением будет | Решение уравнения Лапласа задают в виде суммы шаровых функций второго рода |
|
|
|
так как:
|
Эта функция также:
|
На поверхности иногда заданы не значения функции, а ее нормальные производные. Тогда это задача Неймана, которая также может быть и внутренней и внешней.
Краевое условие в этом случае имеет вид
,
поэтому краевое условие можно записать так:
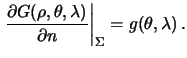
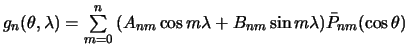-- функция Лапласа.
Поскольку
, для выполнения теоремы Гаусса для
гармонических функций о потоке необходимо, чтобы выполнялось условие
, что эквивалентно условию
.
| Внутренняя проблема Неймана | Внешняя проблема Неймана |
| Нетрудно убедиться, что решением внутренней проблемы Неймана будет | Эту проблему на сфере решает функция |
|
|
|
| Действительно, эта функция гармоническая, так как состоит из суммы шаровых функций первого рода, а подстановка ее в краевое условие (8.9) убеждает нас, что оно выполняется. | В справедливости этого утверждения предлагаем убедить самостоятельно. |
Эта задача, как и две предыдущие может быть и внутренняя, и внешняя. Рассмотрим вариант внешней смешанной краевой задачи, имеющей отношение к теории фигуры Земли. Краевым условием в этом случае будет линейная комбинация самой искомой функции и ее нормальной производной на граничной поверхности
Снова решение будем искать в виде разложения по сферическим функциям
-- сферическая функция, подлежащая определению. Подставим это выражение в краевое
условие (8.12):
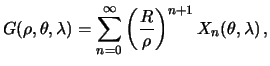
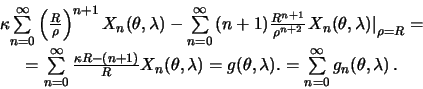
Приравнивая сферические функции одинаковых степеней почленно, получим
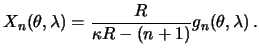
Следовательно, решением внешней смешанной краевой задачи будет
Мы убедились в том, что возмущающий потенциал является гармонической функцией и на сфере выполняется краевой условие (8.6). Это типичная внешняя смешанная краевая задача. Чтобы ее решить, нужно представить смешанную гравитационную аномалию рядом Лапласа
-- сферическое расстояние между точкой
и элементом сферической поверхности
. Представим теперь правую часть уравнения
(8.6), задающее краевое условие.
Для возмущающего потенциала справедливо разложение
,
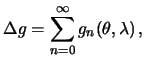
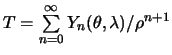где
В классическом решении данной задачи, получившей название задачи Стокса,
предполагается, что масса эллипсоида равна массе реальной Земли, то есть
, а начало координат совпадает с центром масс планеты
Отсюда следует, что разложение возмущающего потенциала
начинается с 
:
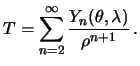
Пренебрегая квадратом сжатия, мы снова дифференцирование по нормали заменим дифференцированием по радиус-вектору
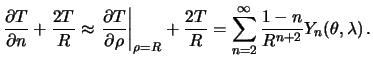
Следовательно
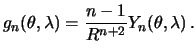
Заметим, что при 
, должно быть
.
Теперь решение краевой задачи для возмущающего потенциала принимает вид
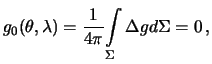
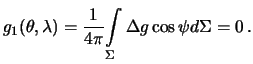
Подставим сюда интегральную форму (8.14) для функций Лапласа:
Поскольку интегрирование ведется по сфере радиуса
в формуле (8.16) мы
полагали 
. Введем обозначение
и решение задачи Стокса принимает окончательный вид
Функцию 
часто называют функцией Стокса.
В (8.17) она задана в виде
разложения по степеням полиномов Лежандра от косинуса центрального
расстояния . Ее "компактный" вид следующий
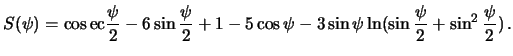
Легко видеть, что точка 
-- особая. Здесь функция Стокса обращается в
бесконечность, тем не менее интеграл
(8.18) сходится, но при выполнении двух
указанных выше условий, которым должны удовлетворять гравитационные
аномалии. Используя формулу (8.1),
которую часто называют формулой Брунса,
из возмущающего потенциала легко получить высоты геоида
Отвесная линия (вертикаль) совпадает с направление вектора силы тяжести g.
Она является нормалью к уровенной поверхности. С другой стороны нормаль к эллипсоиду совпадает с направлением вектора нормальной силы тяжести. Эти две нормали не совпадают. Между ними образуется угол, который геодезисты называют уклонением отвеса. Не будет ошибкой сказать и отклонение отвесной линии. Правда возникает вопрос отклонение от чего? Чтобы таких вопросов не возникало, мы будем употреблять геодезический термин.
Две упомянутые нормали, продолженные вверх, пересекаются с воображаемой небесной сферой в точках, одна из которых будет астрономическим зенитом (или просто зенитом), а другая -- геодезическим. Понятно, что и плоскости горизонта астрономического и геодезического не совпадают. Договорились считать уклонения отвеса положительным, если зенит смещается в северном или восточном направлении.
Обратимся к локальной геодезической системе координат с началом в пункте
наблюдений (точка ). Горизонтальные оси PX и PY,
как мы знаем из лекции 7, лежат
в плоскости, перпендикулярной к нормали к эллипсоиду. Одна из них направлена
на север, другая -- на восток. Ось PZ направлена вниз по внутренней нормали к
эллипсоиду. Нетрудно понять, что при положительных "горизонтальных"
компонентах вектора силы тяжести обе компоненты уклонения отвеса будут
отрицательны. Поэтому компоненты уклонения отвеса в плоскости меридиана и
первого вертикала соответственно определяют следующим образом
Из приведенных формул видно, что обе компоненты -- безразмерные величины, хотя на практике они измеряются в угловых единицах. Дело в том, что уклонения отвеса на Земле составляют секунды дуги, поэтому вместо тригонометрических формул, связывающих уклонения отвеса с компонентами вектора силы тяжести, мы взяли простое отношение.
С другой стороны
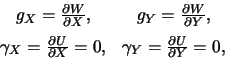
поэтому
Ранее мы видели, что
, поэтому
Формула (8.19) позволяет вычислить высоты геоида,
если на поверхности Земли
заданы смешанные гравитационные аномалии.
Принципиально не имеет значения, в
каких координатах заданы эти аномалии и в каких координатах практически
ведется интегрирование. Мы для этих целей будем применять геодезические
координаты и . Перепишем формулу (8.19)
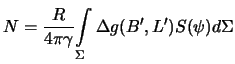
Интегрирование будем выполнять на сфере, а не на эллипсоиде. При этом можно ожидать погрешность в определении высот геоида порядка сжатия. Пренебрегая этими погрешностями, определим элементарные приращения для осей PX и PY
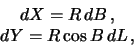
Теперь нужно вычислить производные
и
. Для этого обратимся к формулам
сферической тригонометрии.
Рассмотрим сферический треугольник, который образуют дуги, соединяющие три
точки на сфере: точку , в которой мы хотим определить
уклонение отвеса, точку
-- полюс, и точку -- текущую точку на
поверхности сферы, где расположен
элемент поверхности. Дуга PN равна 90-,
а дуга QN равна 90-
. Угол при
точке равен 
-- азимуту текущей точки Дуга
РР' равна аргументу функции Стокса --
. Угол при полюсе равен разности долгот точки
и точки , то есть 
. Используя
формулы сферической тригонометрии, несложно получить производные угла
по и по , входящие в формулы (8.23)
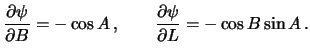
Подставим полученные выражения в (8.23), получим
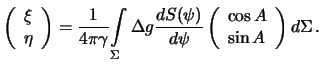
Запишем приведенный интеграл в виде двукратного интеграла. Элемент сферы
равен
,
причем переменная изменяется от 0 до
, а переменная -- от 0 до 
. Получим
Эти формулы носят имя голландского ученого Венинг-Мейнеса. Как и в формулу
Стокса, определяющей высоту геоида точка является устранимой особой
точкой.
На практике используют более сложные методики для вычисления уклонений отвеса с использованием и гравиметрических и геодезических данных.
, что говорит о ее
регулярности на бесконечности.
