Разделы

• 9.1 Критика классической теории Стокса
• 9.2 Система высот
• 9.3 Краевые условия задачи Молоденского

Лекция 9. Квазигеоид Молоденского

Основные трудности решения проблемы Стокса. Проблема регуляризации Земли. Система высот. Геодезическая, ортометрическая и нормальная высоты. Квазигеоид. Аномалия высоты. Теллуроид. Краевые условия задачи Молоденского.

9.1 Критика классической теории Стокса

Применение формулы Стокса для определения высот геоида относительно общего земного эллипсоида наталкивается на серьезные трудности. Во-первых, для интегрирования необходимо, чтобы гравитационные аномалии были известны по всей поверхности Земли, более двух третей которой покрыта морями и океанами. Измерение силы тяжести на поверхности океанов стало возможно лишь в ХХ столетии.

В 1922-1929 годы голландский ученый Ф.А.Венинг-Мейнес работал над созданием аппаратуры для измерения силы тяжести на подвижном основании. Наконец, в 1929 году им был создан окончательный вариант маятникового прибора с которым Венинг-Мейнес совершил плавание на подводной лодке в акваторию юго-восточной Азии, где в то время у Голландии были колонии. Точность гравиметрической съемки ученый оценил в 3-4 мГал, что было достаточно для изучения состояния земной коры в том регионе. На основании этих данных предложил новую теорию изостазии.

Уже в 1930 году заведующий кафедрой гравиметрии механико-математического факультета МГУ профессор Л.В.Сорокин совершил первое плавание в Черном море также на подводной лодке с оригинальной аппаратурой, изготовленной в мастерских ГАИШ. В 1954 году силами института ВНИИГеофизика был создан первый в мире морской гравиметр, а в 1955 году прошел морские испытания на подводной лодке во время плавания вокруг Новой Земли. Результаты убедительно показали, что точность гравиметра не уступает точности маятникового прибора, требует гораздо более простой обработки наблюдений. Маятниковые приборы наземной гравиметрии, как известно, были вытеснены гравиметрами, то же произошло и с морскими приборами. Морские гравиметры сейчас являются основными инструментами морской гравиметрии. Все меньше и меньше остается "белых" пятен на Земле, где сила тяжести неизвестна

Вторая проблема -- более серьезная. Теория Стокса требует, чтобы все массы лежали под уровенной поверхностью, называемой геоидом. Кроме того, измерения силы тяжести выполняются на физической поверхности, не совпадающей с геоидом. Задача состоит в том, чтобы в измеренной значение внести такие поправки, которые бы перенесли все массы под уровень моря, не изменяя самой уровенной поверхности, а сила тяжести оказалась бы отнесенной к уровню моря (геоиду). Эта проблема широко обсуждалась в научной литературе и получила название проблемы регуляризации Земли.

Оказалось, что для успешного решения проблемы регуляризации необходимо знать внутреннее строение Земли. В научный спор о том, как решать проблему регуляризации, в 50-х годах вмешался М.С.Молоденский, который доказал, что различные варианты решения практически эквивалентны, но они не решают задачу вполне строго. Он предложил строгое решение задачи определения фигуры Земли. При этом определяются высоты не поверхности, которую мы называем геоидом, а другой поверхности, достаточно близкой к геоиду, которую он назвал квазигеоидом.

М.С. Молоденский разработал теорию построения квазиеоида, предложил алгоритмы приближенного решения проблемы. Во-первых, редукция (перенос) силы тяжести или потенциала выполняется в линейном приближении. Во-вторых, хотя все измерения и редукции относятся к физической поверхности или к эллипсоиду, интегрирование малых функций, где это требуется, выполняется по сфере (сферическое приближение). Конечно, теория Молоденского не окончательная. Она постоянно совершенствуется его учениками. В Советском Союзе возникла школа Молоденского, которая широко известна не только у нас, но и за рубежом.

9.2 Система высот

Определить фигуру какой-либо поверхности -- это значит определить расстояния каждой точки этой поверхности до тела отсчета, за которое берется эллипсоид вращения. Эти расстояния обычно называют геодезическими высотами. Понятие высоты, на первый взгляд, не требует уточнения. Однако это не так. М.С.Молоденский разработал целую систему высот для геодезии.

Допустим, что имеем две точки и , причем точка выше точки . Если соединить эти точки каналом и пустить воду, куда она потечет? Кажется вполне естественным ответ: из точки к точке . Однако это не совсем так. Весь вопрос в том, как проходит уровенная поверхность через эти точки. Если обе точки лежат на одной уровенной поверхности, то вода никуда не потечет. Если уровенная поверхность, проходящая через точку окажется под уровенной поверхностью точки , то будет наблюдаться обратная картина: вода потечет от точки к точке . Таким образом, для гидротехнических сооружений система геодезических высот оказывается непригодной.

В геодезии высоты определяют нивелированием. Нивелир -- это оптическая труба, визирная линия которой устанавливается строго горизонтально с помощью достаточно высоко чувствительного уровня. Чтобы определить превышение одной точки над другой, в этих точках устанавливаются специальные вертикальные рейки. С помощью нивелира с каждой рейки поочередно берут отсчеты, тогда разность этих отсчетов есть нивелирное превышение одной точки над другой.

Нивелирный ход от точки , расположенной, например, на уровне моря, к точке даст измеренную высоту точки над уровнем моря , где нивелирное превышение одного звена. Если нивелирный ход имеет много звеньев, то сумму можно заменить интегралом .

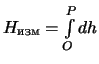Вычислим разность потенциалов меду точками и .

(9.1)

Таким образом, для определения разности потенциалов нужно иметь нивелирные превышения и силу тяжести вдоль всего профиля.

Введем в рассмотрение еще одну точку. Через точку проходит силовая линия, которую можно продолжить до поверхности геоида (уровень моря). Она пересечется с этой поверхностью в токе textitР'. Таким образом точки и Р' лежат на одной поверхности уровня (на геоиде) Поскольку результат определения разности потенциалов не зависит от пути интегрирования, выберем такой маршрут О-Р'-Р. Приращение потенциала мы получим лишь на отрезке силовой линии Р'-Р: 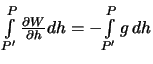. При движении по силовой линии сила тяжести непрерывно меняется. Согласно теореме о среднем, в курсе математического анализа, можно найти такое значение подынтегральной функции, которое она принимает внутри интервала интегрирования, которым можно заменить подынтегральное выражение

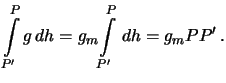
Отрезок силовой линии РР' называется ортометрической высотой точки над уровнем моря (то есть над геоидом). Итак

(9.2)

Чтобы вычислить ортометрическую высоту, необходимо знать не только приращение потенциала, но и уметь вычислить среднее значение силы тяжести на отрезке силовой линии, а для этого необходимо знать как меняется сила тяжести на этом отрезке внутри Земли. М.С.Молоденский предложил заменить на среднее значение нормально силы тяжести. Высоту, которую мы таким образом получим он назвал нормальной. Такая замена неизбежно внесет погрешность, которая, впрочем, невелика. Согласно определению, нормальная высота может быть определена по формуле

(9.3)

Поскольку ортометрическая высота есть высота точки над уровнем моря, то мало отличающаяся от нее нормальная высота будет равна высоте точки от поверхности мало отличающейся от геоида. Молоденский назвал эту поверхность квазигеоидом.

Отличие истинной (геодезической) высоты от нормальной уместно назвать аномалией высоты. Это понятие также ввел Молоденский. Итак, аномалия высоты есть

(9.4)

Аномалия высоты есть расстояние квазигеоида от эллипсоида, или равна высоте почтигеоида. Очевидно, что . В классическом понимании, определить фигуру Земли -- это значит определить высоты геоида . Однако, мы не сделаем большой погрешности, если будем считать фигурой Земли -- фигуру квазигеоида, а для этого мы должны определить аномалии высот.

Сведем задачу снова к краевой задаче для гармонических функций. Следовательно, аномалию высоты нужно определить через возмущающий потенциал (см лекцию 8, раздел 8.1). Итак, имеем:

• потенциал тяжести в точке равен , С -- приращение потенциала от уровня моря (точка );
• нормальный потенциал в точке , равный .

Таким образом, точка не совпадает с точкой , так как она подбирается так, чтобы приращение потенциала реального и нормального были одинаковыми

Здесь постоянные и означают следующее: первая постоянная есть величина потенциала тяжести на геоиде, а вторая -- величина нормального потенциала на уровенном эллипсоиде. Нетрудно убедиться, что отрезок равен аномалие высоты . Следовательно

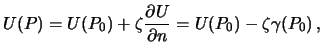
С другой стороны , поэтому

Отсюда следует

(9.5)

Мы получили вновь формулу Брунса, однако она отличается тем, что содержит дополнительный член , который в "классической" формуле отсутствует. В теории Стокса предполагается, что обе эти постоянные равны: потенциал тяжести на уровне моря равен потенциалу уровенного эллипсоида.

Другое отличие: нормальная сила тяжести задается не на геоиде, а в некоторой точке отстоящей от текущей токи на физической поверхности на величину, равную аномалии высоты. Геометрическое место всех точек называется теллуроидом. Гравитационные аномалии, как и прежде, относятся к разным точкам: наблюденное значение задано на физической поверхности, а нормальное -- на теллуроиде.

В литературе, посвященной исследованию гравитационных полей планет, встречаются и другие определения понятия теллуроида, как поверхности аппроксимирующую форму Земли.

Теллуроид Марусси определяется следующим образом. Теллуроид -- геометрическое место точек, в которых потенциал тяжести совпадает с нормальным .

Теллуроид Крарупа (гравиметрический теллуроид) -- геометрическое место точек, в котором нормальная сила тяжести совпадает с силой тяжести на поверхности Земли .

Каждое из определений теллуроида требует своего подхода для определения его фигуры. Мы остановимся здесь лишь на теллуроиде и квазигеоиде Молоденского.

9.3 Краевые условия задачи Молоденского

В точке на физической поверхности Земли нам известно значение потенциала тяжести , а в точке на теллуроиде -- значение нормального потенциала . Используя векторно-матричную математику запишем основные соотношения, связывающие возмущающий потенциал разность потенциалов , так называемую аномалию потенциала, аномалию высоты и смешанную аномалию силы тяжести .

Нетрудно видеть, что на теллуроиде Молоденского , на теллуроиде Марусси , а на теллуроиде Крарупа . В общем случае имеем

(9.6)

Тогда или

(9.7)

Аналогично получим смешанную аномалию

(9.8)

Заметим, что разность , есть так называемая "чистая" аномалия, равна градиенту возмущающего потенциала , поэтому вместо (9.8) можно записать

(9.9)

Итак, мы получили два уравнения, которые на физической поверхности Земли можно взять в качестве краевых условий

(9.10)

Первая из приведенных формул есть обобщение формулы Брунса, связывающей возмущающий потенциал с высотой квазигеоида. Из этих двух уравнений можно построить одно, если исключить аномалию высоты . Решим второе из приведенных уравнений. Предполагая, что матрица неособая, получим . Подставим найденное решение в первое уравнение. Заметим, что

(9.11)

Подставляя полученное выражение в первое уравнение из (9.10), будем иметь

Для упрощения записи, введем обозначение . Теперь краевое условие обобщенной задачи Молоденского принимает вид

(9.12)

9.3.1 Частный случай: измерения выполнены на уровенной поверхности

Рассмотрим случай, когда аномалия потенциала -- постоянная величина. Другими словами точка , как и в задаче Стокса, находится на поверхности уровня. Тогда . Выберем локальную систему отсчета с началом в точке . Ось направим на север, ось -- на восток, а ось -- по направлению внутренней нормали к эллипсоиду вниз. Тогда вектор аномалии высоты может быть определен матрицей-строкой

Градиенты нормального потенциала в точках и равны

Матрица вторых производных нормального потенциала

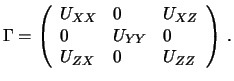
Первое из уравнений (9.10) для краевых условий дает

(9.13)

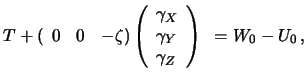
Второе уравнение из (9.10) выглядит следующим образом

(9.14)

Первые два уравнения дают уклонения отвеса

(9.15)

где =206265 -- число секунд в радиане. Последний член в скобках формул (9.15) дает очень малый вклад и может быть отброшен. Действительно, мы видели, что для нормальной силы тяжести максимальное значение горизонтального градиента равно 0,000811 мГал/м. При =100 м, что бывает очень редко, величина составит 0,081 мГал и внесет погрешность в уклонение отвеса 0,017", тогда как уклонения отвеса достигают несколько секунд дуги.

Третье уравнение имеет вид . Подставив сюда величину из (9.13) получим краевое условие для смешанных аномалий

(9.16)

Мы получили, таким образом, краевое условие почти совпадающее с краевым условием Стокса.

Задача определения фигуры Земли сводится к построению решения уравнения Лапласа, которое удовлетворяет краевому условию (9.16) или, в общем случае, условию (9.12). Способы решения этой задачи заслуживают специального изучения, но выходят за пределы нашего курса.