Формула Сомильяны. Нормальная сила тяжести. Вторые производные гравитационного потенциала. Локальное уравнение поверхности уровня. Кривизны и радиусы кривизны нормального сечения поверхности уровня. Вторые производные нормального потенциала. Первые и вторые производные гравитационного потенциала в околоземном пространстве.
Итальянский геодезист Сомильяна (Somigliana) в 1929 году получил точную формулу, показывающую распределение силы тяжести на уровенной поверхности эллипсоида вращения. Вопреки правилам русского языка эта формулa вошла в русскую литературу как формула Сомильяна, как если бы его фамилия была Сомильян. Мы будем склонять его фамилию, поэтому должны назвать его формулу именем Сомильяны.
Как мы видели, потенциал притяжения эллипсоида в
эллипсоидальных координатах ![]() имеет
вид (формула (6.17)):
имеет
вид (формула (6.17)):
Потенциал тяжести отличается тем, что аддитивно включает в себя центробежный потенциал
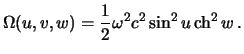
Таким образом
Учитывая, что
![]() , получим
, получим
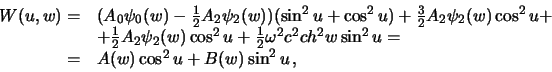
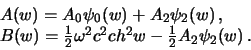
Для того, чтобы получить силу тяжести на поверхности эллипсоида ![]() ,
необходимо продифференцировать функцию
,
необходимо продифференцировать функцию ![]() вдоль координатной линии
вдоль координатной линии
![]() Элемент дуги в этом случае равен
Элемент дуги в этом случае равен
![]() , где
, где ![]() -- коэффициент Ламе,
который, в данном случае, равен
-- коэффициент Ламе,
который, в данном случае, равен
Таким образом, производную потенциала тяжести по нормали к поверхности
эллипсоида ![]() можно записать так
можно записать так
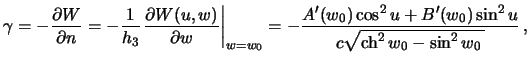
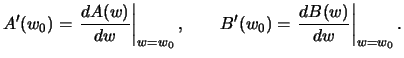
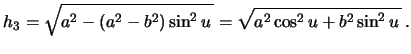
Теперь удельную силу тяжести на поверхности эллипсоида можно записать так
Мы получили искомую формулу для удельной силы тяжести на поверхности
уровенного эллипсоида. Однако нам необходимо избавиться от
постоянных
![]() и
и
![]() .
Заметим, что точка
.
Заметим, что точка ![]() ,
, ![]() соответствует полюсу эллипсоида, а
точка
соответствует полюсу эллипсоида, а
точка
![]() ,
, ![]() -- экватору. Будем снабжать
обозначение для силы тяжести соответственно индексами
-- экватору. Будем снабжать
обозначение для силы тяжести соответственно индексами ![]() и е.
Из (7.2) получим
и е.
Из (7.2) получим
Теперь формулу (7.2) можно переписать следующим образом
Для того, чтобы получить формулу Сомильяны в окончательном виде, необходимо от эллипсоидальной системы координат перейти к геодезической. Сопоставим две системы координат для точек поверхности эллипсоида
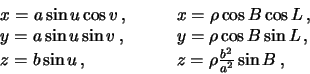
где
![]() (см. лекцию 2, раздел 2.4).
(см. лекцию 2, раздел 2.4).
Поскольку ![]() ( понятия долготы в геодезической и эллипсоидальной системах
координат совпадают), поэтому
( понятия долготы в геодезической и эллипсоидальной системах
координат совпадают), поэтому
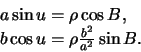
Отсюда
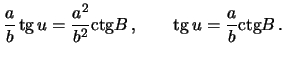
Имеем очевидные выражения для связи ![]() и
и ![]() :
:
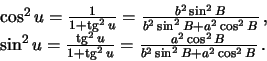
После несложных упрощений, окончательно получим формулу Сомильяны
В геодезии и геофизике основной характеристикой гравитационного поля являются гравитационные аномалии, полученные как разность между наблюденным значением удельной силы тяжести и предвычисленным. Однако сравнивать эти значения можно только, в случае когда наблюденное и нормальное значения относятся к одной и той же точке пространства. В действительности же нормальную силу тяжести относят к общему земному эллипсоиду, а наблюденное -- к физической поверхности Земли. Такие аномалии в геодезии именуют смешанными аномалиями. Иногда наблюденное значение редуцируют, то есть вносят поправки, позволяющие вычислить значение силы тяжести в другой точке или на другой поверхности. При этом используют ту или иную гипотезу о строении верхних слоев Земли. В этом случае понятие гравитационные аномалии уточняют, например гравитационные аномалии в редукции Фая или гравитационные аномалии в редукции Гленни.
Итак, нормальное значение силы тяжести относят к общему земному эллипсоиду, которое можно вычислить по строгой формуле (7.4). Эта формула строгая лишь в том случае, когда поверхность эллипсоида есть поверхность уровня, чего в действительности нет. На практике в задачах геодезии и геофизики применяют приближенную формулу для нормальной силы тяжести. Причем численные значения коэффициентов, входящие в эту формулу, утверждают на Генеральной ассамблее Международного Союза геодезии и геофизики.
Вернемся к формуле Сомильяны. Упростим ее, отбрасывая малые величины порядка
куба сжатия. Введем в обращение понятия геометрического сжатия
![]() и гравитационного сжатия
и гравитационного сжатия
![]() . Обе величины мы будем считать одного порядка малости. В
формуле Сомильяны мы должны заменить
. Обе величины мы будем считать одного порядка малости. В
формуле Сомильяны мы должны заменить ![]() величиной
величиной
![]() , а вместо
, а вместо
![]() взять
взять
![]() :
:
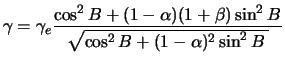
Разлагая полученное выражение в степенной ряд относительно ![]() и
и
![]() , будем иметь
, будем иметь
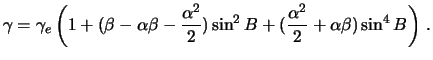
Поскольку
![]() ,
полученная формула принимает вид
,
полученная формула принимает вид
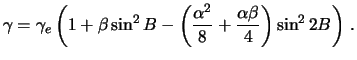
Итак, сила тяжести на поверхности эллипсоида вращения (уровенного) с точностью до малых второй степени относительно сжатия может быть представлена формулой
численные значения коэффициентов
![]() определяются эмпирически.
На Генеральной Ассамблее
Международного Союза, состоявшейся в Москве в 1971 году
рекомендованы следующие значения (сила
тяжести -- в миллигалах)
определяются эмпирически.
На Генеральной Ассамблее
Международного Союза, состоявшейся в Москве в 1971 году
рекомендованы следующие значения (сила
тяжести -- в миллигалах)
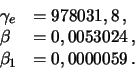
Гравитационный потенциал, а вернее силовая функция для удельной силы тяжести является непрерывной функцией. Принимающей единственное значение в каждой точке пространства. Поверхности равного потенциала (эквипотенциальные поверхности) как угодно плотно заполняют внешнее пространство, нигде не пересекаясь. Вектор силы тяжести в точке P направлен перпендикулярно к эквипотенциальной поверхности, проходящей через эту точку. Таким образом, гравитационный потенциал во внешнем пространстве образует силовое поле. Оно пронизано силовыми линиями, причем направление силы тяжести совпадает с касательной к силовой линии.
Из сказанного следует, что силовые линии не могут пересекаться, так как в точке пересечения не может существовать два вектора силы тяжести. Вектор силы тяжести (удельной) можно записать следующим образом
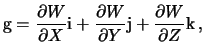
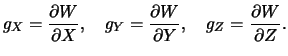
В геодезической и геофизической практике рассматривают также и вторые производные гравитационного потенциала, которые отмечают двойными нижними индексами
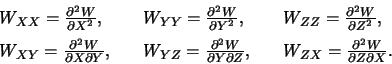
Вторые производные потенциала можно изобразить в виде квадратной матрицы
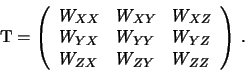
Остается 5 независимых элементов этой матрицы, которая представляет собой тензор вторых производных гравитационного потенциала.
Рассуждения можно продолжить и дальше, образуя третьи производные, четвертые и т.д. Но уже третьи производные нельзя изобразить в виде матрицы: это будет куб размером 3х3, который на двухмерном листе бумаги изобразить трудно. Совершенно невозможно изобразить в виде геометрических фигур производные более высоких порядков. Это будут тензоры высоких валентностей.
Эквипотенциальную поверхность в окрестности точки
![]() можно аппроксимировать плоскостью -- это будет касательная плоскость --
эллипсоидом, гиперболоидом и другими поверхностями второго порядка.
В последнем
случае уравнение этой поверхности будет иметь вид
можно аппроксимировать плоскостью -- это будет касательная плоскость --
эллипсоидом, гиперболоидом и другими поверхностями второго порядка.
В последнем
случае уравнение этой поверхности будет иметь вид
Уравнение касательной плоскости получим, отбрасывая в (7.7) квадратичную форму
где
![]() . Величины
. Величины
![]() -- суть компоненты вектора силы тяжести. Изменяя постоянную
-- суть компоненты вектора силы тяжести. Изменяя постоянную ![]() ,
получим семейство плоскостей, параллельных той, что проходит через точку
P.
,
получим семейство плоскостей, параллельных той, что проходит через точку
P.
Для упрощения выкладок, часто направление местной геодезической системы
выбирают следующим образом: ось PX направляют на север,
ось PY -- строго на
восток, а ось PZ совпадает с вектором
силы тяжести и направлена вертикально
вниз. В этом случае
![]() .
Уравнение(7.8) принимает вид
.
Уравнение(7.8) принимает вид
![]() .
Обозначим приращение
высоты буквой
.
Обозначим приращение
высоты буквой ![]() , получим формулу для вычисления приращения
потенциала
, получим формулу для вычисления приращения
потенциала
![]() , которую часто называют формулой Брунса.
, которую часто называют формулой Брунса.
Определим кривизну нормального сечения уровенной поверхности
![]() . Решим это уравнение относительно
переменной
. Решим это уравнение относительно
переменной ![]() :
: ![]() .
Тогда радиус кривизны
.
Тогда радиус кривизны ![]() в точке
в точке ![]() по формуле Монжа
определяется формулой
по формуле Монжа
определяется формулой
![]() ,
где
,
где ![]() -- угол, который образует ось PX с плоскостью нормального сечения. В
данной формуле буквами
-- угол, который образует ось PX с плоскостью нормального сечения. В
данной формуле буквами ![]() обозначены вторые производные
обозначены вторые производные
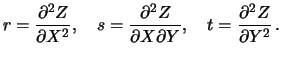
Наша поверхность уровня задана не разрешенной относительно вертикальной
координаты. Поэтому нам нужно получить формулу для кривизны сечения
поверхности, заданной в неявном виде. Продифференцируем зависимость
![]() по одной из координат, например по
по одной из координат, например по ![]() . Тогда
. Тогда
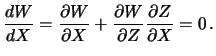
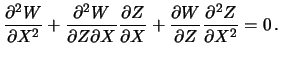
Рассмотрим важные частные случаи:
Итак, вторые производные потенциала тяжести
![]() определяют кривизну (радиус кривизны) нормального сечения уровенной
поверхности. Остается выяснить физический или геометрический смысл еще трех
вторых производных:
определяют кривизну (радиус кривизны) нормального сечения уровенной
поверхности. Остается выяснить физический или геометрический смысл еще трех
вторых производных:
![]() .
.
Поскольку ![]() , то
, то
![]() Горизонтальную компоненту этого градиента называют
горизонтальным градиентом силы тяжести,
а вертикальную компоненту -вертикальным градиентом силы тяжести.
Горизонтальную компоненту этого градиента называют
горизонтальным градиентом силы тяжести,
а вертикальную компоненту -вертикальным градиентом силы тяжести.
Выведем теперь формулу для вертикального градиента силы тяжести. Если точка
![]() внешняя, то справедливо уравнение
внешняя, то справедливо уравнение
![]() . Для внутренней
точки уравнение Лапласа для потенциала притяжения превращается в уравнение
Пуассона, тогда
. Для внутренней
точки уравнение Лапласа для потенциала притяжения превращается в уравнение
Пуассона, тогда
![]() . Перепишем
равенство в наших обозначениях
. Перепишем
равенство в наших обозначениях
Из формул (7.10) и (7.11)
следует, что
![]() ,
,
![]() , поэтому
, поэтому
Мы видим, что для вычисления вертикального градиента силы тяжести необходимо знать радиусы кривизны нормальных сечений уровенной поверхности, плотность и угловую скорость вращения Земли. Наоборот, если нас интересует плотность пород, окружающих точку наблюдения, нужно измерить вертикальный градиент силы тяжести. Поэтому измерение вертикального градиента является очень важной задачей для целей гравитационной разведки.
В заключении, приведем основные формулы для вторых производных нормального
потенциала. Как мы видели, поверхностью уровня в этом случае является
эллипсоид вращения. Радиус кривизны меридионального сечения эллипсоида равен
![]() ,
а сечения в первом вертикале
,
а сечения в первом вертикале
Ограничиваясь малыми порядка сжатия, получим
где ![]() нужно взять из нормальной формулы (7.5).
нужно взять из нормальной формулы (7.5).
Заметим, что
![]() -- достаточно малая
величина. Основной вклад в вертикальный градиент силы тяжести вносит
-- достаточно малая
величина. Основной вклад в вертикальный градиент силы тяжести вносит
![]() . Легко видеть, что вторые производные потенциала по
горизонтальным координатам приблизительно в два раза меньше вертикального
градиента силы тяжести и имеют противоположный знак. Для того, чтобы
привести численные значения коэффициентов в формулу (7.14) необходимо
договорится о единицах измерения. В геофизике принято градиент силы тяжести
измерять в Этвешах, по имени венгерского ученого Лоранда Этвеша, который
создал прибор для измерения вторых производных гравитационного потенциала.
Установлено, что один Этвеш (1 Э) равен градиенту, соответствующему
0,0001 мГал/м или в метрической системе единиц
. Легко видеть, что вторые производные потенциала по
горизонтальным координатам приблизительно в два раза меньше вертикального
градиента силы тяжести и имеют противоположный знак. Для того, чтобы
привести численные значения коэффициентов в формулу (7.14) необходимо
договорится о единицах измерения. В геофизике принято градиент силы тяжести
измерять в Этвешах, по имени венгерского ученого Лоранда Этвеша, который
создал прибор для измерения вторых производных гравитационного потенциала.
Установлено, что один Этвеш (1 Э) равен градиенту, соответствующему
0,0001 мГал/м или в метрической системе единиц
![]() .
.
Прежде, чем привести численные значения, сделаем еще одно замечание. Со
времени Этвеша основным инструментом для измерения вторых производных
потенциала тяжести служит коромысло, на концах которого закреплены на разной
высоте массы. Ось вращения коромысла -- вертикальна. Неоднородность поля
тяжести создает момент, вращающий коромысло, который уравновешивается
моментом упругой силы. Не останавливаясь на подробностях ( это не предмет
обсуждения для нашего курса) укажем лишь, что с этим прибором можно получить
четыре параметра гравитационного поля ![]() ,
, ![]() ,
, ![]() ,
,
![]() .
Приведем численные значения, согласованные с нормальной
формулой для силы тяжести (см. Шокин П.Ф., "Гравиметрия" Геодезиздат, 1960)
.
Приведем численные значения, согласованные с нормальной
формулой для силы тяжести (см. Шокин П.Ф., "Гравиметрия" Геодезиздат, 1960)
При измерении элементов гравитационного поля в космическом пространстве серьезной помехой является невесомость: пробное тело не взаимодействует с опорой и сила, которая действует на пробное тело, не может быть измерена. Однако невесомость, строго говоря, имеет место только в одной точке космического аппарата: в центре масс. Если пробные тела разместить в разных точках космического аппарата, то гравитационные силы будут действовать по-разному. Дифференциальные измерения положения этих пробных тел позволяет получить вторые производные гравитационного потенциала.
Как мы уже говорили, главным препятствием для измерения силы тяжести на борту космического аппарата служит невесомость. Однако существует принципиальная возможность измерять элементы тензора вторых производных потенциала.
Пусть точка ![]() есть точка, совпадающая с центром масс космического аппарата.
Выберем прямоугольную систему координат, связанную с космическим аппаратом
(сопровождающий трехгранник). Начало этой системы координат возьмем в точке
есть точка, совпадающая с центром масс космического аппарата.
Выберем прямоугольную систему координат, связанную с космическим аппаратом
(сопровождающий трехгранник). Начало этой системы координат возьмем в точке
![]() . Направления осей выберем следующим образом:
ось Px направим по касательной к
меридиану, проходящему через точку
. Направления осей выберем следующим образом:
ось Px направим по касательной к
меридиану, проходящему через точку ![]() , ось Py -- на восток,
а ось Pz -- в начало
сферической системы координат, то есть в центр Земли. Пусть
, ось Py -- на восток,
а ось Pz -- в начало
сферической системы координат, то есть в центр Земли. Пусть ![]() --
радиус-вектор точки
--
радиус-вектор точки ![]() ,
, ![]() и
и ![]() --
соответственно геоцентрическая широта и долгота
этой точки. Тогда потенциал притяжения в этой точке будет равен
--
соответственно геоцентрическая широта и долгота
этой точки. Тогда потенциал притяжения в этой точке будет равен
Здесь ![]() и
и ![]() -- стоксовы постоянные. В данном случае мы
центробежный член не учитываем, так как речь идет о потенциале
гравитационного притяжения, а не тяжести.
-- стоксовы постоянные. В данном случае мы
центробежный член не учитываем, так как речь идет о потенциале
гравитационного притяжения, а не тяжести.
Элементарные приращения декартовых координат, очевидно будут
Первые производные гравитационного потенциала по осям сопровождающего трехгранника можно записать в виде дифференциального оператора
Обозначим
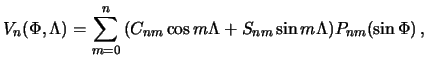
теперь формулу (7.16) можно переписать так
Подставляя полученную формулу в (7.18), будем иметь компоненты градиента
потенциала притяжения на расстоянии ![]() от центра Земли
от центра Земли
Чтобы получить вторые производные потенциала притяжения, необходимо каждую
из компонент силы притяжения продифференцировать по трем координатным осям.
При вычислении вторых производных нельзя пользоваться формулами линейной
связи элементарных приращений координат (7.17), как мы это делали при
вычислении первых производных. Самый очевидный путь (но не самый легкий!)
-- прямое дифференцирование функции
![]() как неявную
функцию переменных
как неявную
функцию переменных ![]() . Однако он связан с громоздкими выкладками.
. Однако он связан с громоздкими выкладками.
Наша цель -- показать как изменяются вторые производные потенциала с
увеличением расстояния до спутника. Поэтому ограничимся лишь второй
радиальной производной потенциала. Силовая линия для этой координаты --
прямая линия, поэтому учитывать ее кривизну не требуется. Дифференцируя
потенциал, заданный формулой (7.19), по координате ![]() , получим
, получим
Мы видим, что после дифференцирования каждый член разложения потенциала
приобретает коэффициент, растущий с увеличением степени как ![]() Таким
образом, множитель
Таким
образом, множитель
![]() указывает,
что с повышением "частоты" увеличивается
и множитель, точно так же, как и при спектральном разложении функции
времени. Таким образом, дифференцирующий эффект увеличивает "верхние"
гармоники разложения потенциала.
указывает,
что с повышением "частоты" увеличивается
и множитель, точно так же, как и при спектральном разложении функции
времени. Таким образом, дифференцирующий эффект увеличивает "верхние"
гармоники разложения потенциала.
Однако, одновременно с этим эффектом существует и "интегрирующий" эффект:
с увеличением расстояния ![]() множитель
множитель
![]() уменьшает амплитуду
гармоники. Поэтому возникает вопрос, какие гармоники и на какой высоте
следует определять при планировании космического эксперимента.
уменьшает амплитуду
гармоники. Поэтому возникает вопрос, какие гармоники и на какой высоте
следует определять при планировании космического эксперимента.
Английский ученый Каула экспериментально показал, что амплитуды сферических
гармоник потенциала убывают с возрастанием степени ![]() как
как ![]() . С другой
стороны амплитуды гармоник второй производной потенциала увеличиваются как
. С другой
стороны амплитуды гармоник второй производной потенциала увеличиваются как
![]() . Следовательно гармоники вторых производных в широком диапазоне
частот имеют характер "белого шума". Но с увеличением высоты благодаря
интегральному эффекту верхний диапазон частот оказывается подавленным.
. Следовательно гармоники вторых производных в широком диапазоне
частот имеют характер "белого шума". Но с увеличением высоты благодаря
интегральному эффекту верхний диапазон частот оказывается подавленным.
Выполним простейший расчет "частотной характеристики" преобразования
сферических гармоник потенциала в гармоники радиальной второй производной на
высоте ![]() .
.
Пусть ![]() , где
, где ![]() -- высота полета спутника над планетой. В качестве
характеристики подавления гармоники степени
-- высота полета спутника над планетой. В качестве
характеристики подавления гармоники степени ![]() , очевидно, можно принять
, очевидно, можно принять
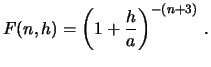
Приведем таблицу значений ![]() при различных высотах и степеней гармоник.
при различных высотах и степеней гармоник.
| h | 200 км | 500 км | 1000 км | 5000 км |
|---|---|---|---|---|
| n | ||||
| 2 | 0.86 | 0.68 | 0.48 | 0.055 |
| 4 | 0.80 | 0.59 | 0.36 | 0.017 |
| 6 | 0.76 | 0.51 | 0.27 | 0.005 |
| 8 | 0.71 | 0.44 | 0.20 | - |
| 10 | 0.67 | 0.37 | 0.15 | - |
| 20 | 0.49 | 0.18 | 0.035 | - |
| 50 | 0.19 | 0.018 | -- | - |
| 100 | 0.041 | -- | -- | - |
Таблица показывает, что для выполнения задачи измерения вторых производных
годятся лишь очень низкие спутники. Причем на высоте 200 км от гармоник
степени и порядка 100 остается лишь около 4%. Это означает, что если на
поверхности Земли нас может удовлетворить точность 1% от амплитуды
аномалий градиента, то в космических условиях мы будем вынуждены требовать
точность на два порядка выше. Следовательно, в качестве приемлемой точности
измерения мы должны планировать чувствительность приборов не менее 0,001Э,
что эквивалентно градиенту ![]() мГал/м
мГал/м
![]() g/м.
Такой высокой чувствительности в земных условиях вряд ли
можно достигнуть. Однако в космосе, в условиях глубокого вакуума и
сверхнизких температурах надежда на успех остается.
g/м.
Такой высокой чувствительности в земных условиях вряд ли
можно достигнуть. Однако в космосе, в условиях глубокого вакуума и
сверхнизких температурах надежда на успех остается.