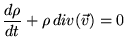

След.: Общие уравнения для малых
Выше: Магнитогидродинамические волны.
Пред.: Магнитогидродинамические волны.
Для начала напомним основные формулы гидродинамики идеальной жидкости
Это уравнение непрерывности :
Уравнение Эйлера:
Условие изоэнтропийности движения:
Закон сохранения энергия:
Напомним также, что под
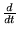 в данном случае понимается оператор
субстанциональной производной, т.е. производная берется в точке жестко
привязанной к частице жидкости
При наличии магнитного поля возникают объемные силы действующие на
жидкость - силы Лоренца. Она равна:
в данном случае понимается оператор
субстанциональной производной, т.е. производная берется в точке жестко
привязанной к частице жидкости
При наличии магнитного поля возникают объемные силы действующие на
жидкость - силы Лоренца. Она равна:
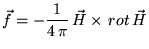 |
(5) |
Мы будем рассматривать жидкость без объемных зарядов, поэтому в формуле для
силы Лоренца нет члена с напряженностью
электрического поля. Напомним, что в хорошо проводящей
жидкости электрическим полем, по сравнению с магнитным можно пренебречь.
Также к уравнениям гидродинамики добавляются 2 уравнения для
магнитного поля.
root
2003-04-25