Резюме. Проводится интерпретация источников аномалий гравитационного поля. Точечные источники располагаются под крупнейшими аномалиями геоида. Определяются их координаты, массы и предельные глубины расположения. Такой анализ позволяет установить, могут ли источники, вызывающие крупнейшие гравитационные аномалии, располагаться внутри земного ядра. Необходимым условием для такого вывода является то, чтобы предельные глубины оказались больше глубины границы ядро-мантия.
В силу некорректности задачи существует множество различных интерпретаций источников, вызывающих отклонение гравитационного поля Земли от поля гидростатически уравновешенной Земли (например, [1-2], как наиболее типичные). Проблема интерпретации становится вполне корректной, если мы ограничим ее определением координат, масс и предельных (максимальных) глубин расположения крупнейших источников. Такой анализ позволит определить, могут ли источники, вызывающие крупнейшие гравитационные аномалии, располагаться внутри земного ядра. Необходимым условием для такого вывода является то, чтобы предельные глубины оказались больше глубины границы ядро-мантия.
Чтобы решить поставленную задачу, мы должны представить источники как точечные массы или сферически-симметричные структуры, поскольку любое другое представление формы источника, отличное от сферически-симметричного, может только уменьшать глубину расположения источника. Чтобы определить параметры таких точечных масс, необходимо решить систему уравнений, минимизирующую следующее среднеквадратичное уклонение:
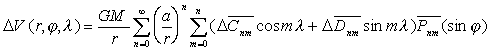 -
(2)
-
(2)неравновесная часть гравитационного потенциала Земли, представленная в виде разложения по шаровым функциям;
сумма гравитационных потенциалов источников; ![]() - сферические координаты точки наблюдения; G - универсальная постоянная;
M, a - масса и средний экваториальный радиус Земли;
- сферические координаты точки наблюдения; G - универсальная постоянная;
M, a - масса и средний экваториальный радиус Земли; ![]() -
нормализованные гармонические коэффициенты неравновесного поля Земли;
-
нормализованные гармонические коэффициенты неравновесного поля Земли; ![]() -
массы точечных источников и их расстояние от точки наблюдения; I - общее
число источников;
-
массы точечных источников и их расстояние от точки наблюдения; I - общее
число источников; 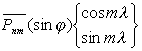 -
нормализованные сферические функции.
-
нормализованные сферические функции.
Используя в (3) известные разложения [4]:
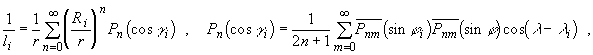
где ![]() -
сферические координаты источников, можно получить следующее выражение для
U:
-
сферические координаты источников, можно получить следующее выражение для
U:
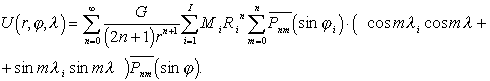
Поскольку система шаровых функций ортогональна всюду на
и вне сферической поверхности, то минимум (1) будет достигнут всюду во
внешнем пространстве, если ![]() удовлетворяют следующей системе уравнений:
удовлетворяют следующей системе уравнений:
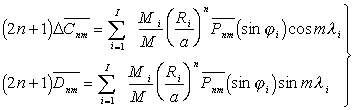 (4)
(4)для ![]() ,
где N характеризует степень сглаженности. Исходной информационной величиной,
определяющей N, можно принять среднюю горизонтальную протяженность
,
где N характеризует степень сглаженности. Исходной информационной величиной,
определяющей N, можно принять среднюю горизонтальную протяженность ![]() крупнейших
гравитационных аномалий -
крупнейших
гравитационных аномалий - ![]() .
.
Если выделить источники, влияющие только на зональные гармоники потенциала, то система (4) преобразуется в следующую простую систему:
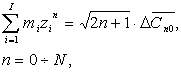 (5)
(5)
В качестве исходных данных для неравновесной части (2) гравитационного потенциала Земли мы рассматривали 4 варианта:
1) общее неравновесное поле Земли:
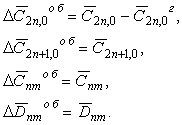
Здесь ![]() -
спутниковые значения гармонических коэффициентов, взятые нами из одной
из последних моделей [6];
-
спутниковые значения гармонических коэффициентов, взятые нами из одной
из последних моделей [6]; ![]() -
гармонические коэффициенты гравитационного поля Земли, находящегося в состоянии
гидростатического равновесия, где
-
гармонические коэффициенты гравитационного поля Земли, находящегося в состоянии
гидростатического равновесия, где ![]() взяты
нами из [7, стр. 74-75];
взяты
нами из [7, стр. 74-75];
2) в общем неравновесном
поле Земли учтено влияние масс рельефа планеты, компенсированного на некоторой
глубине ![]() :
:
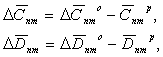
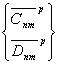 -
вклад изостатически компенсированного рельефа в гравитационное поле Земли.
-
вклад изостатически компенсированного рельефа в гравитационное поле Земли.
Если принять схему компенсации по Эри-Хейсканену, т.е. осуществлять компенсацию по принципу баланса масс рельефа и компенсирующих масс, то можно записать (в линейном приближении):
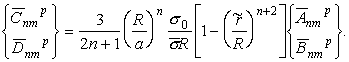 (6)
(6)Здесь ![]() -
коэффициенты разложения высот рельефа
-
коэффициенты разложения высот рельефа ![]() относительно
принятой поверхности относительности (гидростатически уравновешенного эллипсоида
Земли):
относительно
принятой поверхности относительности (гидростатически уравновешенного эллипсоида
Земли):
![]()
![]() -
средний радиус поверхности рельефа,
-
средний радиус поверхности рельефа, ![]() -
средний радиус поверхности относительности,
-
средний радиус поверхности относительности, ![]() где
где ![]() -
средняя глубина компенсации,
-
средняя глубина компенсации, ![]() -
средняя плотность масс рельефа,
-
средняя плотность масс рельефа, ![]() -
средняя плотность Земли.
-
средняя плотность Земли.
При получении (6) использовались формулы для потенциала
простого слоя, приведенные в [4, стр. 260]. Для параметров использовались
следующие численные значения: ![]() =6371.03
км,
=6371.03
км, ![]() =2.
67
=2.
67 ![]() ,
, ![]() =5.517
=5.517![]() .
Для
.
Для ![]() использовалось
разложение эквивалентного (т.е. однородного по плотности) рельефа, полученное
в [8], относительно гидростатического эллипсоида Земли.
использовалось
разложение эквивалентного (т.е. однородного по плотности) рельефа, полученное
в [8], относительно гидростатического эллипсоида Земли. ![]() =22.37
км - средняя глубина поверхности компенсации (поверхности Мохоровичича)
- взята из [9];
=22.37
км - средняя глубина поверхности компенсации (поверхности Мохоровичича)
- взята из [9];
3) в общем неравновесном поле Земли учтено влияние масс эквивалентного рельефа Земли и масс, обусловленных формой границы Мохоровичича:
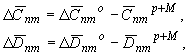
В линейном приближении (т.е. при замене масс рельефа и границы Мохоровичича простым слоем) можно записать:
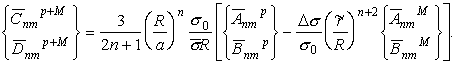 (6)
(6)Здесь ![]() =0.34
=0.34![]() -
наиболее вероятный средний скачок плотности на границе Мохоровичича,
-
наиболее вероятный средний скачок плотности на границе Мохоровичича, ![]() -
коэффициенты разложения глубин d поверхности Мохоровичича относительно
той же поверхности относимости, что и для эквивалентного рельефа:
-
коэффициенты разложения глубин d поверхности Мохоровичича относительно
той же поверхности относимости, что и для эквивалентного рельефа:
Для ![]() использовалось
разложение глубины поверхности Мохоровичича, полученное в [9] на основе
сейсмических данных и приведенное к гидростатическому эллипсоиду Земли.
использовалось
разложение глубины поверхности Мохоровичича, полученное в [9] на основе
сейсмических данных и приведенное к гидростатическому эллипсоиду Земли.
4) в общем неравновесном
поле Земли учтено влияние масс рельефа и М, гидростатически уравновешенных
на некоторой глубине ![]() ,
(т.е. введена гипотеза о компенсации путем выравнивания давления на глубине
,
(т.е. введена гипотеза о компенсации путем выравнивания давления на глубине ![]() ).
).
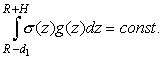
Если принять, что такое выравнивание осуществляется в
верхней мантии на глубине границы фазового перехода I рода ![]() =660
км, то при g(z)=const
=660
км, то при g(z)=const
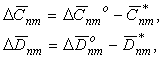
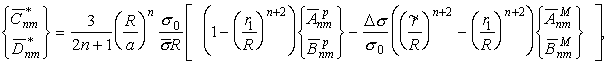 где
где Чтобы выявить возможные источники, лежащие в ядре, мы
использовали для анализа только низкие гармоники гравитационного поля Земли.
Причем, чтобы исключить неоднозначность решения системы (4) при произвольном
выборе координат источников ![]() ,
мы располагали источники под крупнейшими аномалиями геоида. Координаты
центра аномалий определялись на основе карты высот геоида, построенной
для данного номера разложения N. На рис.1, рис.2,
рис.3 и рис.4 приведены
карты высот геоида, соответствующих разным исходным данным I-4, в таблице
1 - параметры источников, полученные из решения системы (4) и соответствующие
1 и 4 картам.
,
мы располагали источники под крупнейшими аномалиями геоида. Координаты
центра аномалий определялись на основе карты высот геоида, построенной
для данного номера разложения N. На рис.1, рис.2,
рис.3 и рис.4 приведены
карты высот геоида, соответствующих разным исходным данным I-4, в таблице
1 - параметры источников, полученные из решения системы (4) и соответствующие
1 и 4 картам.
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
||||
Автор выражает благодарность доктору физ-мат. наук Чуйковой Н.А. за полезные обсуждения работы.
Работа выполнена при финансовой поддержке РФФИ, грант 94-05-16784.
1. П.А.Мещеряков. Задачи теории потенциала и обобщенная Земля. Москва, Наука, 1991.
2. Ю.А.Тараканов и др. Отклонение от гидростатического равновесия Земли и Луны. Физика Земли, 1985, №8, с.3-27.
3. Н.А.Чуйкова, Н.В.Алахвердова. Земное ядро как общий источник гравитационных и магнитных аномалий: предварительные результаты //Труды ГАИШ, т.65, с.96.
4. Г.Н.Дубошин. Теория притяжения. Москва, Госиздат,1961.
5. Н.А.Чуйкова, С.А.Казарян. Учет внутреннего строения Земли при интерпретации альтиметрических данных.// Вестник МГУ, Серия Физика, Астрономия", 1994, с.
6. A geopotential model from satellite tracking, altimeter and surface gravity data: GEM-T3 // J.Geophys.Res.,vol.99, no.B2, pages 2815-2839, February 10, 1994.
7. В.Н.Жарков, В.П.Трубицын, П.В.Самсоненко. Физика Земли и планет. Москва, Наука, 1971.
8. Н.А.Чуйкова, А.Н.Грушинский, Т.Г.Максимова. Гармонический и статистический анализ эквивалентного рельефа Земли и его изостатическая компенсация // Труды ГАИШ, т.65, с.51
9. Н.А.Чуйкова, Т.Г.Максимова. Гармонический и статистический анализ глубин поверхности Мохоровичича// Труды ГАИШ, т.65, с.33