Резюме. Решена задача о влиянии оболочки земного ядра на полярные колебания твердого ядра Земли. Рассматривались две модели оболочки: первая получена на основе внешнего гравитационного поля Земли путем исключения влияния приповерхностных слоев Земли, вторая строилась на основе сейсмических данных о топографии границы ядро-мантия. Получены уточненные (по сравнению с Шлихтером и Буссе) формулы для частоты колебаний и проведены численные расчеты. Оказалось, что выбор модели мало влияет на частоту колебаний (период колебаний Т1= 4 часа 22 минуты 22 секунды, Т2= 4 часа 22 минуты 38 секунд) и значительно влияет на смещение ядра (-0.32 км для первой модели и 0.26 км для второй).
Будем исследовать движение твердого внутреннего ядра Земли
вдоль оси вращения в следующей модели. Внутреннее ядро будем считать однородным
и сферическим с плотностью ![]() i,
массой mi и радиусом ri. Оно погружено
в однородное жидкое ядро с плотностью
i,
массой mi и радиусом ri. Оно погружено
в однородное жидкое ядро с плотностью ![]() e,
массой me и ограничено сферической границей радиуса re.
Будем рассматривать такие медленные движения твердого ядра, что для вычисления
распределения давления в жидком ядре в каждый момент времени можно пользоваться
уравнением гидростатического равновесия. Ось вращения совместим с осью
Oz прямоугольной декартовой системы координат с началом в центре
Земли и осями, жестко связанными с ней. Уравнение движения твердого ядра
представим в виде:
e,
массой me и ограничено сферической границей радиуса re.
Будем рассматривать такие медленные движения твердого ядра, что для вычисления
распределения давления в жидком ядре в каждый момент времени можно пользоваться
уравнением гидростатического равновесия. Ось вращения совместим с осью
Oz прямоугольной декартовой системы координат с началом в центре
Земли и осями, жестко связанными с ней. Уравнение движения твердого ядра
представим в виде:
A) ![]() U=U3-U2-U1,
U=U3-U2-U1,
где U3 - гравитационный потенциал всей Земли, известный, например, из спутниковых наблюдений; U2 - потенциал гидростатически уравновешенной Земли; U1 - потенциал изостатически компенсированного рельефа.
Б) Основное влияние на движение ядра оказывают массы,
расположенные на границе ядро-мантия. Поэтому можно представить потенциал ![]() U
силы F1 как потенциал простого слоя, расположенного на границе ядро-мантия
с плотностью:
U
силы F1 как потенциал простого слоя, расположенного на границе ядро-мантия
с плотностью:
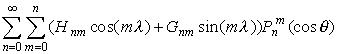 ,
,В обоих случаях ![]() U
во внешнем пространстве представляется в виде разложения по шаровым функциям
вида:
U
во внешнем пространстве представляется в виде разложения по шаровым функциям
вида:
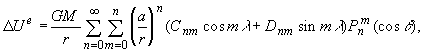 (2)
(2)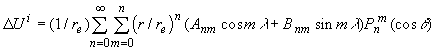 .
(3)
.
(3)Так как исследуется движение твердого ядра вдоль оси Oz, то полагая здесь z=r, найдем
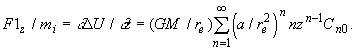 (5)
(5)
Рассмотрим такие движения внутреннего ядра, при которых можно приближенно считать, что в каждый момент выполнены условия гидростатического равновесия. Начало системы координат в этом случае удобно совместить с центром твердого ядра, находящимся в точке z=-a в старой системе координат. Тогда силовая функция в расчете на единицу массы
где: U1-силовая функция жидкого шара радиуса | r' -a|
c центром в точке z' =a; U2 - силовая функция шара с плотностью ![]() i-
i-![]() e
с центром в точке r' =0 и радиусом ri .
e
с центром в точке r' =0 и радиусом ri .
В этом случае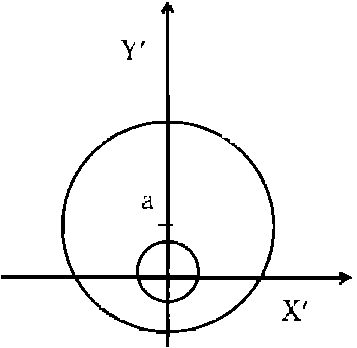 r'
-a=(
r'
-a=(![]() '
cosj' ,
'
cosj' , ![]() '
sinj' , z' -a ), откуда
'
sinj' , z' -a ), откуда
nz' =cos![]() '
, z'на поверхности твердого ядра= ricos
'
, z'на поверхности твердого ядра= ricos![]() '?
,
'?
,
dSна поверхности твердого ядра=
ri2sin![]() '
,
(12)
'
,
(12)
Обозначим через z' z -координату, через r'
- модуль радиус-вектора точки в старой системе координат. Тогда
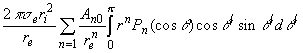 .
(14)
.
(14)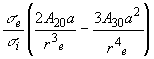 +С3
(18)
+С3
(18)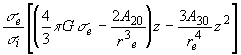 .
(19)
.
(19)Подставляя (19),(5), и (6) в (1) и учитывая основные действующие
силы, получим
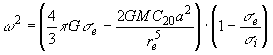 ,
, 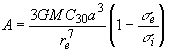 ,
,
где медленно меняющиеся функции B и ![]() определяются дифференциальными уравнениями:
определяются дифференциальными уравнениями:
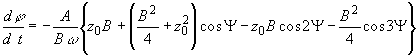 ,
,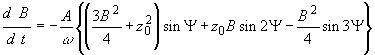 , (24)
, (24)Для количественных оценок были приняты следующие значения
постоянных, соответствующих модели стандартной Земли:
a =6.378![]() 106м,
re =3.4774
106м,
re =3.4774![]() 106
м, ri =1.2215
106
м, ri =1.2215![]() 106м
,
106м
, ![]() e
=12
e
=12![]() 103
кг/м3 ,
103
кг/м3 ,
GM=398 603![]() 109м3/с2,
G=6.6742
109м3/с2,
G=6.6742![]() 10-11м3/(кг
10-11м3/(кг![]() с2),
с2), ![]()
![]() e=
e=![]() i-
i-![]() e=597
кг/м3. Было рассмотрено
два случая. В случае A коэффициенты получены в результате обработки данных
спутниковых наблюдений [1], а в случае Б коэффициенты
e=597
кг/м3. Было рассмотрено
два случая. В случае A коэффициенты получены в результате обработки данных
спутниковых наблюдений [1], а в случае Б коэффициенты ![]() получены
из
получены
из ![]() по
формуле [2]:
по
формуле [2]:
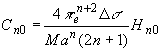 ,
,|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
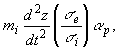
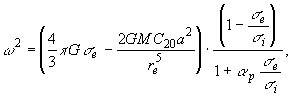
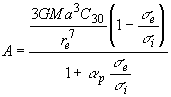
Из сравнения (A) и (Б) можно заключить, что модель внешней оболочки мало влияет на период колебаний внутреннего ядра Земли и лишь влияет на величину смещения положения равновесия внутреннего ядра.
Работа выполнена при финансовой поддержке РФФИ, грант 94-05-16784.
1)A geopotential model from satellite tracking, altimeter and surface gravity data: GEM-T3 // J. Geophys.Res., vol.99, no. B2, pages 2815-2839, february 10, 1994.
2) Дубошин Г.Н. Теория притяжения // Государственное издательство физ.-мат. литературы, с. 260.
3) Казарян С.А. Земное ядро как источник гравитационных аномалий //Труды ГАИШ, том LXY, 1996, с. 86
4) F.H.Busse. On the oscillation of the Earth's Inner Core // J. Geophys. Res., 79, 753,1974.
5) Б.М.Яновский. Земной магнетизм // из-во Ленинградского университета. 1964.
6) L.B.Slichter. The fundamental free mode of the Earth's inner core // Proc. Nat. Acad. Scien.USA,186,1961.
7) H.Lamb. Hydrodynamics 6th ed.. //p 125 , Dover New York , 1945.