Резюме. Исследуется задача корреляционной зависимости между аномалиями гравитационного и магнитного полей при наличии общих источников различной формы и происхождения, лежащих во внешнем ядре Земли или на его границе.
Получены формулы для гравитационного и магнитного потенциалов таких источников. Разработана оригинальная методика поиска корреляционной зависимости для источников, лежащих на общей оси. Методики проверены на конкретных моделях гравитационного и магнитного полей, полученных из наблюдений.
The formulas of gravity and magnetic potentials of such sources are received. The original method of search of correlative dependence for the sources, laying in the common axis is worked out. The method is tested using the concrete models of Earth gravity and magnetic fields, base on the observations.
Существующие в настоящее время гипотезы происхождения особенностей главного магнитного поля Земли связывают их в основном с конвективными движениями во внешнем ядре Земли. Однако наличие таких движений свидетельствует о наличии плотностных неоднородностей во внешнем ядре Земли, что должно отразиться и в гравитационном поле Земли.
Попытки найти связь между особенностями гравитационного и магнитного полей Земли предпринимались рядом исследователей [1-7]. Однако к определенным выводам прийти не удалось. Причина этого, как нам представляется, заключается в следующих обстоятельствах, связанных с природой этих полей:
1) В гравитационное поле Земли вносят значительный вклад неоднородности строения коры и мантии Земли, которые никак не отражаются в главном магнитном поле Земли. Поэтому поиски корреляционных зависимостей между гравитационным и магнитным полями Земли могут не привести к положительным результатам. Прежде чем сравнивать эти поля, необходимо предварительно удалить из гравитационного поля влияние коры и мантийных источников, т.е. решить задачу разделения гравитационных полей.
2) Характер корреляционных связей между гравитационным
и магнитным полями зависит от физической природы источников, вызывающих
магнитные и гравитационные аномалии. Под магнитными аномалиями мы здесь
понимаем отклонение ![]() U
главного магнитного поля Земли от поля центрального диполя:
U
главного магнитного поля Земли от поля центрального диполя:
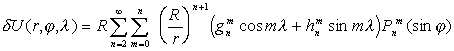 , (1)
, (1)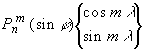 - сферические функции. (Вопрос о нормировке мы пока не рассматриваем.)
- сферические функции. (Вопрос о нормировке мы пока не рассматриваем.)
Под гравитационными аномалиями мы здесь понимаем отклонение ![]() V
внешнего гравитационного поля Земли от поля гидростатически уравновешенного
эллипсоида Земли:
V
внешнего гравитационного поля Земли от поля гидростатически уравновешенного
эллипсоида Земли:
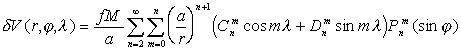 ,
(2)
,
(2)где а - экваториальный радиус Земли, ![]() -
гармонические коэффициенты неравновесного гравитационного поля Земли.
-
гармонические коэффициенты неравновесного гравитационного поля Земли.
Гармонические коэффициенты можно выразить через распределение намагниченности и плотности внутри Земли:
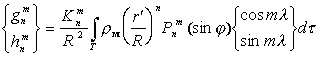 , (3)
, (3)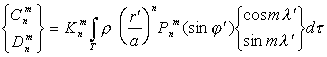 . (4)
. (4)Здесь ![]() ,
, ![]() .
.
Таким образом, только в случае линейной зависимости между ![]() и
и ![]() , а,
следовательно, и линейной зависимости между гармоническими коэффициентами
одной степени и порядка, можно обнаружить корреляцию между гравитационным
и магнитным полями. Однако рассмотрение даже простейшего примера: однородного
по плотности и однородного по намагниченности шара, показывает, что такой
линейной зависимости нет:
, а,
следовательно, и линейной зависимости между гармоническими коэффициентами
одной степени и порядка, можно обнаружить корреляцию между гравитационным
и магнитным полями. Однако рассмотрение даже простейшего примера: однородного
по плотности и однородного по намагниченности шара, показывает, что такой
линейной зависимости нет:
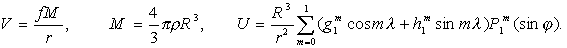
Таким образом, однородный шар вносит вклад в нулевую гармонику гравитационного потенциала, но для магнитного потенциала - в гармоники первой степени в системе координат, начало которой совмещено с центром шара.
Рассмотрим теперь более подробно поставленную задачу.
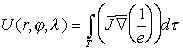 ,
(5)
,
(5)Если зафиксировать направление вектора намагниченности ![]() ,
то (5) можно легко преобразовать к выражению (1).
,
то (5) можно легко преобразовать к выражению (1).
Рассмотрим следующие варианты.
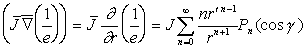 ,
,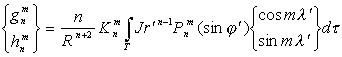 ,
,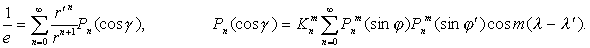
Сравнивая (6) и (4), мы видим, что только при J ![]()
![]()
![]() получим
линейную зависимость между гармониками магнитного и гравитационного потенциала:
получим
линейную зависимость между гармониками магнитного и гравитационного потенциала:
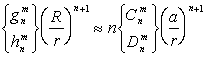 . (7)
. (7)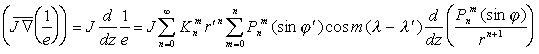 ,
,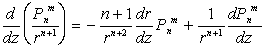 ,
,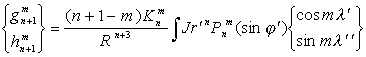 .
(8)
.
(8)Сравнивая (8) и (4), мы видим, что из J ![]()
![]() следует:
следует:
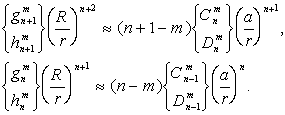 (9)
(9)Рассмотрим теперь источники, расположенные на сферической
поверхности S' фиксированного радиуса ![]() .
В этом случае как магнитное, так и гравитационное поле можно представить
в виде потенциала простого слоя, расположенного на сфере:
.
В этом случае как магнитное, так и гравитационное поле можно представить
в виде потенциала простого слоя, расположенного на сфере:
![]() - потенциал
магнитного поля, где n - нормаль к S',
- потенциал
магнитного поля, где n - нормаль к S',
![]() - плотность
магнитного момента, которую можно также выразить через силу I тока элементарного
контура, расположенного на S' ,
- плотность
магнитного момента, которую можно также выразить через силу I тока элементарного
контура, расположенного на S' , 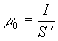 ,
т.е. через токовую функцию:
,
т.е. через токовую функцию:
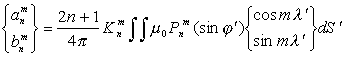 .
.1) Если все магнитные моменты ориентированы вдоль радиуса ![]() сферы
S' , т.е. элементарные контуры тока расположены на сферической поверхности
S', то тогда можно получить следующие соотношения:
сферы
S' , т.е. элементарные контуры тока расположены на сферической поверхности
S', то тогда можно получить следующие соотношения:
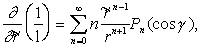
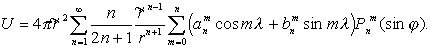 (10)
(10)Сравнивая (10) и (1), мы видим, что в этом случае коэффициенты разложения плотности магнитного момента следующим образом выражаются через гармонические коэффициенты магнитного потенциала:
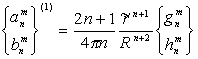 . (11)
. (11)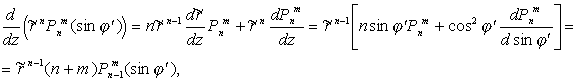
Сравнивая (12) и (1), мы видим, что в этом случае коэффициенты разложения плотности магнитного момента следующим образом выражаются через гармонические коэффициенты потенциала:
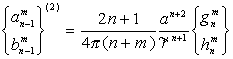 или
или 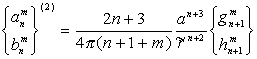 (13)
(13)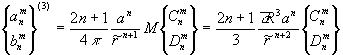 , (15)
, (15)Таким образом, если ![]() ,
то из соответствия
,
то из соответствия ![]() следует
корреляция между коэффициентами (11) и (15), а если
следует
корреляция между коэффициентами (11) и (15), а если ![]() ,
то из соответствия
,
то из соответствия ![]() следует
корреляция между коэффициентами (13) и (15).
следует
корреляция между коэффициентами (13) и (15).
Полученные нами результаты свидетельствуют о том, что можно найти линейную зависимость между гармоническими коэффициентами гравитационного и магнитного потенциала, а, следовательно, можно обнаружить и корреляцию между этими полями только в случае, когда намагниченность всех источников имеет одинаковую направленность. Поскольку реальные источники, по-видимому, не подчиняются данному условию, к тому же в гравитационное поле дают вклад и источники, не отраженные в магнитном поле, то мы разработали следующую методику поиска общих источников.
Как известно, источники, лежащие вдоль или симметрично полярной оси Земли, вносят максимальный вклад в зональные гармоники потенциала, все остальные источники - в тессеральные и секториальные гармоники. Поэтому, выделяя из разложения (1) только зональные члены, можно найти параметры источников, центры которых лежат вдоль полярной оси. Определяя затем коэффициент корреляции между зональными гармониками гравитационного и главного магнитного полей
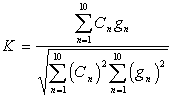 , (17)
, (17)Чтобы аналогичным образом выявить общие источники, центр
которых вне полярной оси, мы осуществили повороты системы координат на
произвольные углы и затем определяли зональные коэффициенты в новой системе
координат с полярной осью, задаваемой координатами ее полюса ![]() .
Определить же зональные гармоники для повернутой новой системы координат
можно на основе теоремы сложения для обобщенных сферических функций [10]
:
.
Определить же зональные гармоники для повернутой новой системы координат
можно на основе теоремы сложения для обобщенных сферических функций [10]
:
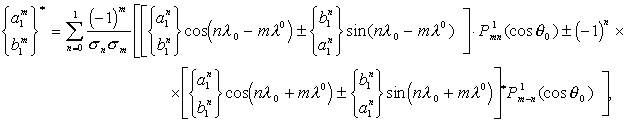
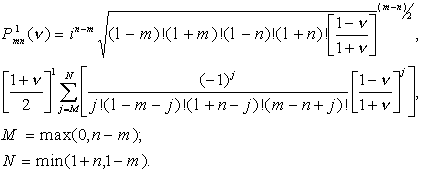
Зная величины зональных гармоник в системе координат, полюс полярной оси которой совпадает с местом экстремального коэффициента корреляции, полученным на основе карты, можно определить параметры источника, а именно его форму, массу и глубину залегания. Внизу мы приводим таблицу значений зональных гармоник как для гравитационного, так и для магнитного полей для разных видов источников.
|
|
|
|
| 1. точечный источник массы m,
смещенный на расстояние z от начала координат
|
1. диполь (или шар)
момента М, смещенный на z |
|
| 2. диск радиуса а, массы m, смещенный
на z |
2. намагниченный диск
или токовое кольцо 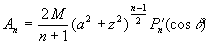 |
|
| 3. полушар a, z |
3. полушар a, z |
|
4. цилиндр
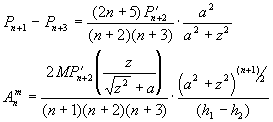 |
4. намагниченный цилиндр
или токовая цилиндрическая поверхность.
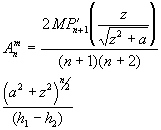 |
|
5. шаровой сектор 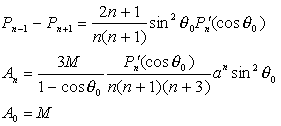 |
5. намагниченный шаровой
сектор
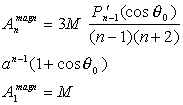 |
|
6. конус
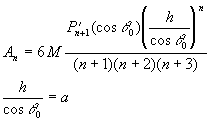 |
6. намагниченный сплошной конус
или токовая коническая поверхность
|
|
7. сплюснутый эллипсоид
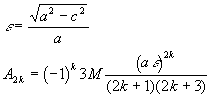 |
7. сплюснутый эллипсоид
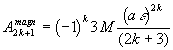 |
|
8. вытянутый эллипсоид
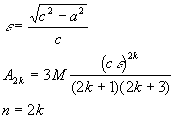 |
8. вытянутый эллипсоид
|
|
9. однородный отрезок
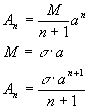 |
9. однородный отрезок или разнесенный
диполь
|
|
где вид функции ![]() выбирается
из таблицы, можно определить параметры источников заданной формы.
выбирается
из таблицы, можно определить параметры источников заданной формы.
Рис.1 Существует около 18-ти
источников (структур), центры которых расположены на расстоянии ![]() ,
они вызывают сильную корреляцию ( | к | > 0.6) между гравитационным и магнитным
полями этих источников, причем как положительную, так и отрицательную.
Максимальная корреляция (к
,
они вызывают сильную корреляцию ( | к | > 0.6) между гравитационным и магнитным
полями этих источников, причем как положительную, так и отрицательную.
Максимальная корреляция (к ![]() -0.9
-0.9 ![]() -1) отмечена
для координат:
-1) отмечена
для координат: ![]() = 20°,
= 20°, ![]() =
80° ,
=
80° , ![]() =
-25° ,
=
-25° , ![]() =
270° . Характеристики корреляции и координат источников практически не
меняются при увеличении разложения от n=4 до n=8.
=
270° . Характеристики корреляции и координат источников практически не
меняются при увеличении разложения от n=4 до n=8.
Рис.2 В общем картина подобна
рис.1, что свидетельствует о превалировании вклада
зональных гармоник в характер корреляции, что подтверждает вывод о наличии
общих источников, расположенных в местах экстремумов коэффициентов корреляции.
Отмечены те же источники с максимальной корреляцией (к ![]() -0.9
-0.9![]() -1)
-1) ![]() = 20° ,
= 20° , ![]() = 80° ,
= 80° , ![]() = -25° ,
= -25° , ![]() = 270° , не исчезают при увеличении степени разложения n = 4
= 270° , не исчезают при увеличении степени разложения n = 4![]() 10.
10.
Рис.3, Рис.4
Выявлены регионы сильной корреляции для низких гармоник n ![]() 4. Почти для всех них наблюдается максимальная корреляция |к=0.9| . Всего
таких районов около 19. При учете гармоник более высоких степеней корреляция
уменьшается, причем гораздо сильнее для случая
4. Почти для всех них наблюдается максимальная корреляция |к=0.9| . Всего
таких районов около 19. При учете гармоник более высоких степеней корреляция
уменьшается, причем гораздо сильнее для случая ![]() || r. Для низких гармоник зоны корреляции, чередуясь по знаку, имеют в
основном широтное простирание.
|| r. Для низких гармоник зоны корреляции, чередуясь по знаку, имеют в
основном широтное простирание.
Сравнивая карты коэффициентов корреляции для простого слоя с картами простого слоя гравитационного и магнитного полей можно обнаружить два вероятных общих источника этих полей:
1) для случая ![]() || r приблизительное расположение этих источников
|| r приблизительное расположение этих источников ![]()
![]() -50° ,
-50° , ![]()
![]() 30° и
30° и ![]()
![]() 7° ,
7° , ![]()
![]() 120° ; первому источнику (к=-0.9) соответствует положительная гравитационная
аномалия и отрицательная магнитная, второму источнику (к=+0.9) соответствует
положительная гравитационная аномалия и нулевая магнитная.
120° ; первому источнику (к=-0.9) соответствует положительная гравитационная
аномалия и отрицательная магнитная, второму источнику (к=+0.9) соответствует
положительная гравитационная аномалия и нулевая магнитная.
2) для случая ![]() ||
z, местоположение вероятных общих источников гравитационного и магнитного
полей:
||
z, местоположение вероятных общих источников гравитационного и магнитного
полей: ![]()
![]() 50° ,
50° , ![]()
![]() 20° и
20° и ![]()
![]() 50° ,
50° , ![]()
![]() 190°
190° ![]() 195°
, здесь первому источнику (к=-0.9) отвечает положительная гравитационная
аномалия и положительная магнитная, а второму (к=+0.9) соответствует нулевая
гравитационная аномалия и положительная магнитная.
195°
, здесь первому источнику (к=-0.9) отвечает положительная гравитационная
аномалия и положительная магнитная, а второму (к=+0.9) соответствует нулевая
гравитационная аномалия и положительная магнитная.
Рис.5 Здесь наблюдается
гораздо больше источников с max корреляцией (как отрицательной, так и положительной)
в отличие от рис.1. Наблюдается положительная корреляция между всеми гармониками
одинаковой степени гравитационного и магнитного полей при повороте системы
координат в направлении ![]() q
= 70° ,
q
= 70° , ![]() = 300° - северный полюс,
= 300° - северный полюс, ![]() = -60° ,
= -60° , ![]() = 110° - северный полюс и отрицательная корреляция при
= 110° - северный полюс и отрицательная корреляция при ![]() =
60° ,
=
60° , ![]() =
120°
=
120° ![]() 220°
,
220°
, ![]() = -60°
,
= -60°
, ![]() = 300°
= 300° ![]() 400° . В этих районах корреляция сохраняется при n = 4 .. 10. Все другие
локальные регионы тоже сохраняются по знаку, хотя несколько уменьшаются
по величине. Если посмотреть карты гравитационного и магнитного полей,
то они отвечают максимальной гравитационной силе и нулевой магнитной.
400° . В этих районах корреляция сохраняется при n = 4 .. 10. Все другие
локальные регионы тоже сохраняются по знаку, хотя несколько уменьшаются
по величине. Если посмотреть карты гравитационного и магнитного полей,
то они отвечают максимальной гравитационной силе и нулевой магнитной.
Работа выполнена при поддержке Российского фонда фундаментальных
исследований, грант 94-05-16784.
1. Почтарев В.И. О некоторых общих чертах магнитного и гравитационного полей Земли //Исследования по геомагнетизму, аэрономии и физике Солнца, 1973, Выпуск 27.
2. Луговенко В.Н. О разделении геомагнитного поля на аномальную и нормальную составляющие // Наука, 1969.
3. Tan-wen Wang (China) // Physics of the Earth and Planetary Interiors 44, 1986, 319-323.
4. Hide R., Maline S. // Nature, 1970, v.225, 5233.
5. Почтарев В.И. Магнитное поле Земли и фигура геоида // Труды НИИЗМ, Москва, 1970, вып.5.
6. Житимов О.А. О корреляции аномального гравитационного и недипольного магнитного полей Земли // Тезисы доклада, 4 Всесоюзный съезд по Геомагнетизму "Магнитные и электрические поля твердой Земли", Суздаль, 1991.
7. Почтарев В.И. Нормальное магнитное поле Земли // Москва, Наука, 1984, ИЗМИРАН.
8. Яновский Б.М. Земной магнетизм, ЛГУ, 1978.
9. Дубошин Г.Н. Теория притяжения, Москва, 1961.
10. Чуйкова Н.А. О преобразованиях ряда Лапласа при поворотах системы координат // Вестник МГУ, сер. Физика, Астрономия, 1983, т.24, № 6, стр. 75-78.
11. Peddie N.W. International Geomagnetic Reference Field 1980 // A report by IAGA Division 1 Working Group 1, J. Geomagnetic and Geoelectric, 1981, 33, 607-611.
12. Бойков В.П., Демьянов Т.П., Галазин В.Ф.// Геодезия и картография, 1992, 4, с.4.