Резюме. Решена задача о движении Солнца в Галактике и рассчитана орбита Солнца для современной модели гравитационного потенциала Галактики. Проведён фурье-анализ зависимости частоты инверсий магнитного поля Земли за 550 млн. лет от времени. При сопоставлении палеомагнитных данных с результатами расчёта орбиты Солнца выявлены следующие закономерности: частота инверсий геомагнитного поля максимальна при прохождении Солнечной системы через те области Галактики, где в максимальной степени изменяется гравитационный потенциал и физические свойства окружающей среды, а именно, при выходе Солнца из спиральных рукавов Галактики, при пересечении Солнцем плоскости Галактики и при наименьшем расстоянии Солнца от центра Галактики.
Для уточнения полученных закономерностей и выяснения их
причин нужны дальнейшие исследования.
To specify received regularities and to find out their causes further investigations are needed.
Данная статья посвящена решению весьма интересной задачи: временной зависимости глобальных геодинамических явлений от положения Земли в Галактике. В частности, исследователи геологического и геомагнитного прошлого Земли заметили, что в геодинамической активности Земли проявляются некоторые периодичности, соответствующие движению Солнечной системы относительно центра и плоскости Галактики.
а) Из исследований остаточной намагниченности пород известно, что магнитное поле Земли неоднократно меняло свою полярность. Обращения происходят нерегулярно, но, в среднем, интервал между ними составляет 200000 лет, а само обращение длится 10-25 тыс. лет. Вообще же интервалы между инверсиями составляют от 30 тыс. до 30 млн. лет (например, 235 — 290 млн. лет назад поле на протяжении почти 60 млн. лет имело обратную полярность). Во время инверсии напряжённость поля уменьшается в 5-7 раз ([1] , [2] ).
В общей картине инверсий выделяются некоторые закономерности, которые можно увидеть из графика нормированного фурье-спектра величины ПП/ОП (рис. 1), где ПП - количество интервалов с прямой полярностью, ОП - количество интервалов с обратной полярностью; ПП/ ОП вычислялась по интервалам длительностью в 15 млн. лет. На графике видны 2 основные гармоники с периодом в 260 - 340 и 70 - 90 млн. лет ([3] ).
б) Сходные периоды прослеживаются и в геологической истории Земли. Выделяют период в 215 млн. лет, состоящий из 4 циклов продолжительностью в 30, 50, 85 и 50 млн. лет. В ходе первого цикла происходит глобальное похолодание, общее поднятие материков, увеличивается сейсмическая и вулканическая активность. В третьем цикле - глобальное потепление, столкновения литосферных плит, колебательные движения на устойчивых блоках земной коры. Второй и четвёртый циклы - промежуточные [4] .
Авторы указанных выше работ не нашли внутренних, земных источников такой периодичности, но предположили, что она связана с движением Солнца в Галактике, т.к. период обращения Солнца вокруг центра Галактики - 240 млн. лет, а период колебаний в направлении, перпендикулярном диску - 80 млн. лет.
Целью работы является проверка и уточнение отмеченных закономерностей в свете современных данных о строении Галактики.
Наша Галактика относится к спиральным галактикам. Её масса ![]() г.
В Галактике обычно выделяют 3 компоненты: диск, балдж и гало. Балдж — центральное
утолщение размером 1 кпк. Диск - самая массивная компонента, его масса
г.
В Галактике обычно выделяют 3 компоненты: диск, балдж и гало. Балдж — центральное
утолщение размером 1 кпк. Диск - самая массивная компонента, его масса![]() .
Толщина диска в окрестности Солнца - 0.5 кпк, радиус диска - 20 кпк. В
диске существуют два спиральных рукава, которые вращаются твердотельно
с угловой скоростью
.
Толщина диска в окрестности Солнца - 0.5 кпк, радиус диска - 20 кпк. В
диске существуют два спиральных рукава, которые вращаются твердотельно
с угловой скоростью![]() =
25 км/ с
=
25 км/ с![]() кпк. Диффузное
вещество (пыль, газ) концентрируется главным образом в рукавах. Диск быстро
вращается вокруг центра Галактики.
кпк. Диффузное
вещество (пыль, газ) концентрируется главным образом в рукавах. Диск быстро
вращается вокруг центра Галактики.
Солнце находится в диске на расстоянии 8.2 кпк от центра
Галактики и отстоит от плоскости Галактики на 25 пк. Круговая скорость
центроида околосолнечных звёзд v0= 220
км/с. Скорость Солнца относительно центроида ![]() км/
с ([5] ).
км/
с ([5] ).
Чтобы прояснить вопрос о влиянии Галактики на земные процессы,
надо рассчитать орбиту Солнца в Галактике. Будем делать это в несколько
этапов. Сначала рассчитаем орбиту в регулярном поле, то есть без учёта
влияния рукавов и различных неоднородностей. Потом учтём влияние рукавов.
Ну а далее попытаемся учесть влияние близких массивных объектов, возможные
колебания ядра Галактики и другие эффекты.
Задачу будем решать в цилиндрической системе координат
(r,![]() ,z). Предположим,
что потенциал Галактики не зависит от
,z). Предположим,
что потенциал Галактики не зависит от ![]() и симметричен относительно плоскости Галактики: U=U(r,z).
и симметричен относительно плоскости Галактики: U=U(r,z).
Уравнения Лагранжа запишутся тогда следующим образом:
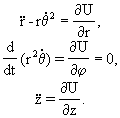 (* )
(* )Будем искать решение системы в виде почти круговой орбиты
в линейном приближении. Мы можем это сделать, т.к. ![]() <<1.
В качестве нулевого приближения возьмём круговую орбиту (1):
<<1.
В качестве нулевого приближения возьмём круговую орбиту (1):
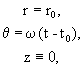 (1)
(1)Подставляя (1) в (*), получим:
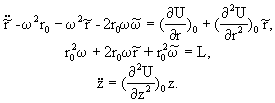
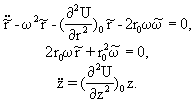
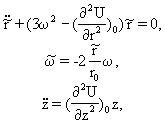
Решение этих систем можно записать в следующем виде:
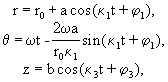 где
где 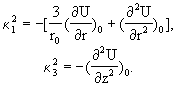 (3)
(3)Величины ![]() определяются
из начальных условий.
определяются
из начальных условий.
Согласно (3), вдоль оси Z происходят гармонические колебания.
Для определения проекции возмущённой орбиты на плоскость Галактики перейдём
в систему координат с центром на круговой орбите, вращающуюся вокруг центра
Галактики с угловой скоростью ![]() .
.
В этой системе
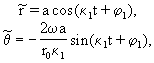 где
где Отсюда следует: 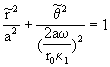 .
.
Значит в плоскости Галактики возмущённое движение происходит
по эллипсу. Для этого эллипса исторически принято название эпицикл.
Для расчёта была взята модель Галактики из работы [6].
Потенциал ![]() ,
где
,
где ![]() - потенциал
в центре Галактики;
- потенциал
в центре Галактики;
— безразмерный потенциал; ![]() —
уравнение эквипотенциали;
—
уравнение эквипотенциали; ![]() - параметры конкретной
- параметры конкретной
Галактики; ![]() ;
; ![]() —
масштабный параметр.
—
масштабный параметр.
Уравнение эквипотенциали записывается в виде: ![]() ,
где
,
где 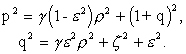 (6)
(6)
Используя параметры нашей Галактики ![]() [7],
[7],
получим: ![]() ,
а
,
а ![]() .
.
Очевидно, что
Пусть ![]() .
Тогда
.
Тогда ![]() -
точка на круговой орбите.
-
точка на круговой орбите.
Дифференцируя (5) и (6) и подставляя ![]() получим:
получим:
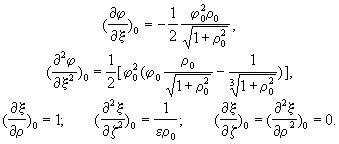 (7)
(7)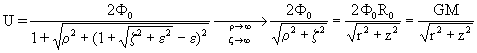 ,
(8)
,
(8)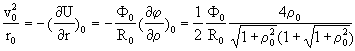 . (9)
. (9)Выражаем ![]() из
(7) и подставляем в (8):
из
(7) и подставляем в (8):
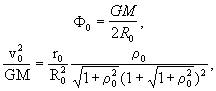 (10)
(10)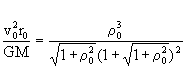 .
(11)
.
(11)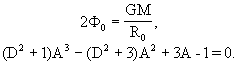 (12)
(12)Подставляя полученные значения в (7), найдём:
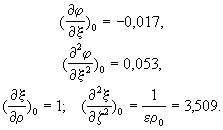 (13)
(13)Эти величины согласуются с результатами изучения кинематики звёзд. Это естественно, поскольку любая модель Галактики должна соответствовать наблюдениям в окрестности Солнца.
Найдём амплитуды и фазы колебаний Солнца относительно круговой орбиты, принимая за t=0 наше время.
а) Движение по z-координате (относительно плоскости
Галактики) Используя полученные из наблюдений данные [5]: z(0) = 25 пк, ![]() (0)
= 6 км/с, получим из (3):
(0)
= 6 км/с, получим из (3):
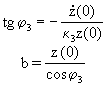 .
.Отсюда b=69 пк, ![]() 3=
-1,2 рад, что соответствует
3=
-1,2 рад, что соответствует ![]() Т=
-14 млн. лет (современное положение Солнца относительно максимума).
Т=
-14 млн. лет (современное положение Солнца относительно максимума).
Следовательно, Солнце пересекало плоскость Галактики 4, 41,78, 115... млн. лет назад; находилось на максимальном удалении от плоскости Галактики 23, 60, 97, 134... млн. лет назад.
б) Движение по r и ![]() (по эпициклу)
(по эпициклу)
Используя полученные из наблюдений данные: ![]() км/с,
км/с, ![]() км/с
, получим из (3):
км/с
, получим из (3):
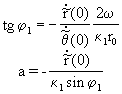 .
.Значит, 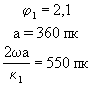 .
.
![]() 1=2,1
рад соответствует Т=60 млн. лет (современное положение Солнца относительно
максимального удаления от круговой орбиты).
1=2,1
рад соответствует Т=60 млн. лет (современное положение Солнца относительно
максимального удаления от круговой орбиты).
Следовательно, Солнце находилось на максимальном удалении от центра Галактики 60, 240, 420, 600... млн. лет назад; Солнце находилось на минимальном расстоянии от центра Галактики 150, 330, 510, 690... млн. лет назад.
Теперь определим, когда Солнце пересекало спиральные рукава. Будем моделировать их логарифмической спиралью:
![]() ,
где j = 1, 2 - номер рукава,
,
где j = 1, 2 - номер рукава, ![]() =
6,1 кпк,
=
6,1 кпк, ![]() =
10,3 кпк,
=
10,3 кпк, ![]()
![]() tg i = tg 9° ,6 ([8] ).
tg i = tg 9° ,6 ([8] ).
Рукава твердотельно вращаются вокруг центра Галактики
с угловой скоростью ![]()
![]() 24км
24км![]() с/кпк. Время пересечения Солнцем
рукавов определим из системы уравнений:
с/кпк. Время пересечения Солнцем
рукавов определим из системы уравнений:
В системе отсчёта, вращающейся вместе с рукавом:
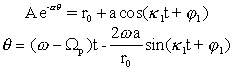 .
.Решая это уравнение для первого рукава методом деления отрезка пополам, получим 3 корня:
Чтобы уточнить полученные моменты времени, надо учесть
гравитационное поле рукавов.
Получив некоторые сведения об орбите Солнца, попытаемся выявить связь между его движением в плоскости Галактики и геомагнитными явлениями.
В [9] приведён график зависимости доли состояний со смешанной полярностью от времени. Он интерпретируется как зависимость скорости обращений от времени (рис. 2). Значительное увеличение скорости обращений примерно 500 млн. лет назад, может быть, связано с выходом Солнца из рукава.
Для отыскания более тонких эффектов нами был проведён фурье-анализ этого графика (рис. 3 и рис. 4).
Пусть функция f(t) задана на сетке Г ={-T=t1<t2 <...<tn=0}, где n нечётно. При помощи замены переменных x=t/T получим сетку Г1={-1=x1<x2< <...<xn=0}. Сгладим f(x) на отрезке [-1,1] параболами, используя для этого интерполяционную формулу Лагранжа :
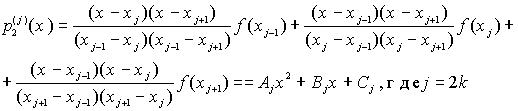 .
.Составим функцию 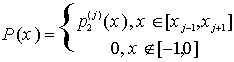 .
Фурье-образ функции P(x) и примем в качестве фурье-образа исходной
функции f(x).
.
Фурье-образ функции P(x) и примем в качестве фурье-образа исходной
функции f(x).
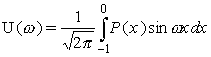 —
синус-компонента фурье-образа, а
—
синус-компонента фурье-образа, а 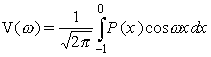 —
его косинус-компонента.
—
его косинус-компонента.
Тогда ![]()
Вычислим амплитуды и фазы образа на некоторой сетке ![]() ,
а потом сгладим их параболами и исследуем полученные функции на экстремум.
,
а потом сгладим их параболами и исследуем полученные функции на экстремум.
Для решения задачи была написана программа на языке Турбо-Паскаль 7.0.
Результаты анализа (амплитуды и фазы максимумов) представлены в таблице 1.
| Ф( |
Ф( |
Т( |
W( |
| 1,6 | 97 | 380 | 5,50 |
| 1,5 | 55 | 230 | 3,00 |
| -0,9 | -21 | 150 | 5,25 |
| -1,3 | -25 | 120 | 2,85 |
| -0,55 | -8 | 94 | 1,25 |
| 0 | 0 | 79 | 1,20 |
| 0,2 | 2 | 69 | 1,20 |
Период в 230 млн. лет соответствует периоду обращения Солнца вокруг центра Галактики.
Гармоника с периодом в 79 млн. лет, соответствующая периоду колебаний вдоль оси Z, принимает свои экстремальные значения, когда Солнце пересекает плоскость Галактики.
Гармоника с периодом в 150 млн. лет, соответствующая периоду движения по эпициклу, была близка к своему максимуму, когда Солнце находилось на минимальном расстоянии от центра Галактики; а когда оно было на наибольшем удалении от центра Галактики, то гармоника была близка к минимуму.
Все расчёты носят оценочный характер. Однако нам известно,
что ошибки исходных данных (сведений о строении Галактики, палеомагнитных
данных) не меньше 10-20 % , значит и точность полученных здесь результатов
примерно того же порядка.
При сопоставлении палеомагнитных данных с результатами расчёта орбиты Солнца в Галактике выявлены следующие соответствия.
1. Во время выхода Солнца из спирального рукава Галактики частота инверсий геомагнитного поля увеличилась.
2. Частота инверсий магнитного поля Земли увеличивается, когда Солнце либо пересекает плоскость Галактики, либо находится на наименьшем расстоянии от её центра.
Для уточнения найденных закономерностей и выяснения их причин нужны дальнейшие исследования.
Работа выполнена при поддержке РФФИ, грант № 94-05-16784.