Резюме. Проведено разложение высот поверхности r эквивалентного рельефа Земли по сферическим функциям до степени N=30 и его сравнение с рельефом поверхности Мохоровичича (М) и с гравитационным полем Земли. Основные результаты:
1) средний радиус r составляет 6369.62 км,
2) геометрический центр r смещен относительно центра
масс Земли на 1.04 км в направлении точки с координатами: ![]() ;
;
3) полярное сжатие r составляет 0.00329, экваториальное сжатие равно 0.00017;
4) компенсация рельефа, соответствующая гармоникам степени, больше 3, осуществляется в среднем на глубинах, меньше, чем глубины поверхности Мохо, а соответствующая n=1,2 - на больших глубинах;
5) значительное отличие полярного сжатия геоида (0.003352) от сжатий поверхности эквирельефа и гидростатической поверхности (0.003337) объясняется большим сжатием мантии Земли (0.0048);
6) Оценка глубин М на основе гипотезы изостатической компенсации рельефа возможна только для неровностей М большой протяженности, характеризующихся разложением степени N=10 и меньше. Оценка глубин М на основе корреляции их с аномалиями Буге не подтверждается.
1) the mean radius of r is 6369.62 km;
2) the r figure center is displaced from the Earth
center at the distance of 1.04 km in the direction ![]() ;
;
3) the polar r flattening is 0.00329, the equatorial one is 0.00017;
4) isostatic compensation of topography exists on the depths less then M depths for degree more or equal 3, and deeper for degree equal 1 and 2;
5) the difference between the geoid flattenings and the r and hydrostatic flattenings is caused by the large M flattenings;
6) the estimation of the Moho depths by means of the correlation
with the Bouguer anomalies are not confirmed. The estimation on the basis
of the isostatic compensation hypothesis is possible only for large-scale
Moho extension, which are characterized by the expansion of 10 degree and
less.
Для учета вклада приповерхностных масс в гравитационное поле Земли, а так же для проверки гипотезы изостатической компенсации масс рельефа необходимо иметь модель поверхности эквивалентного (т.е. однородного по плотности) рельефа. В настоящее время мы располагаем двумя опубликованными моделями рельефа, которые можно было бы использовать для этих целей:
1) разложение высот эквивалентного рельефа (относительно геоида) по сферическим функциям, выполненное G.Balmino, K.Lambeck, W.Kaula в 1973 г. и представленное в [1] в виде таблицы гармонических коэффициентов до 8-ой степени разложения;
2) разложения высот поверхности литосферы и поверхности Земли до уровня гидросферы (относительно геоида), выполненные А.М.Щербаковым в 1983 г. и представленные в [2] в виде таблицы гармонических коэффициентов до 30-ой степени разложения.
Чтобы получить гармонические коэффициенты разложения высот эквирельефа по сферическим функциям на основе разложения Щербакова мы использовали следующую формулу:
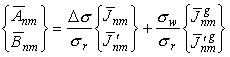 ,
(1)
,
(1)где ![]() г/см3
- средняя плотность масс эквивалентного рельефа;
г/см3
- средняя плотность масс эквивалентного рельефа; ![]() г/см3
- средняя плотность морской воды;
г/см3
- средняя плотность морской воды; ![]() ;
; 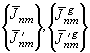 -
нормированные гармонические коэффициенты разложения высот поверхности литосферы
и поверхности Земли до уровня гидросферы соответственно.
-
нормированные гармонические коэффициенты разложения высот поверхности литосферы
и поверхности Земли до уровня гидросферы соответственно.
Сравнение полученных таким образом коэффициентов разложения эквивалентного рельефа и коэффициентов, приведенных в [1], показало, что отличие между величинами коэффициентов для некоторых гармоник достигает 50 % их значения и для нескольких гармоник коэффициенты отличаются даже по знаку. По-видимому, такое отличие можно объяснить абсолютно различными массивами исходных данных, полученных различными службами (США и СССР) с различными точностями и с разной степенью покрытия поверхности Земли наблюдениями. Для выявления причин отличия нами были построены карты высот эквивалентного рельефа по двум моделям (1 - Balmino, 2 - Щербакова) для разложения N=8:
На приведенной на рис.1 карте
разностей высот ![]() видно,
что максимальные отличия соответствуют Антарктиде и прилегающим к ней морям
(
видно,
что максимальные отличия соответствуют Антарктиде и прилегающим к ней морям
(![]() км для N=8
).
км для N=8
).
Очевидно, также отличие вызвано плохим качеством или отсутствием
данных для этих областей в опубликованных моделях [1,2]. Поэтому мы решили
усовершенствовать модель эквирельефа, уточнив на основе современных данных
высоты эквивалентного (приведенного по другой терминологии) рельефа Антарктиды
и прилегающих морей (![]() ).
Кроме того, в настоящее время стало возможным уточнить так же аналогичные
данные для эквирельефа Евразии (
).
Кроме того, в настоящее время стало возможным уточнить так же аналогичные
данные для эквирельефа Евразии (![]() ).
).
Для Евразии при расчете эквирельефа учитывались известные
плотностные неоднородности в верхах земной коры (осадочные бассейны). Для
этого были необходимы данные о глубинах фундамента и средневзвешенных плотностях
осадочной толщи. Данные о глубинах фундамента были в основном взяты с карты
масштаба 1 : 2 500 000 под редакцией В.В.Семенович, Л.И.Ровнина, Н. В.Неволина,
В.Ю.Зайченко и др., изданной в 1982 году, на которой дан рельеф поверхности
фундамента для платформенных областей СССР [3]. На этой карте для детально
изученных структур изогипсы проведены через 0.1![]() 0.2км,
а в районах со слабой геолого-геофизической изученностью (глубокие малоизученные
впадины) - через 1.0
0.2км,
а в районах со слабой геолого-геофизической изученностью (глубокие малоизученные
впадины) - через 1.0![]() 2.0км. Степень
достоверности данных не указана. Для дальневосточных морей и сопредельных
территорий использовались данные со структурных карт, взятых из отчета
Сахалин НИПИнефтегаз (1984) и выполненных под руководством В.В.Харахинова
[4]: 1) Тектоническая карта дальневосточных морей и сопредельных территорий,
масштаб 1: 2 500 000, 2) Тектоническая карта. Охотоморский регион, масштаб
1: 1 500 000. Для остальной части изучаемой территории использовались данные
о рельефе фундамента с карты рельефа поверхности фундамента Евразии масштаба
1: 15 000 000, составленной под руководством Н.Я.Кунина и вышедшей в 1987
году [5]. Эти данные были дополнены сведениями из многочисленных публикаций.
На карте Н.Я.Кунина изогипсы даны с сечением
2.0км. Степень
достоверности данных не указана. Для дальневосточных морей и сопредельных
территорий использовались данные со структурных карт, взятых из отчета
Сахалин НИПИнефтегаз (1984) и выполненных под руководством В.В.Харахинова
[4]: 1) Тектоническая карта дальневосточных морей и сопредельных территорий,
масштаб 1: 2 500 000, 2) Тектоническая карта. Охотоморский регион, масштаб
1: 1 500 000. Для остальной части изучаемой территории использовались данные
о рельефе фундамента с карты рельефа поверхности фундамента Евразии масштаба
1: 15 000 000, составленной под руководством Н.Я.Кунина и вышедшей в 1987
году [5]. Эти данные были дополнены сведениями из многочисленных публикаций.
На карте Н.Я.Кунина изогипсы даны с сечением ![]() км
и указана степень достоверности данных (изолинии в районах с прогнозными
данными даны пунктиром).
км
и указана степень достоверности данных (изолинии в районах с прогнозными
данными даны пунктиром).
Для вычисления эквирельефа необходимо иметь данные о средневзвешенных
значениях плотности осадочного чехла, осредненных по площадям ![]()
Эти данные готовились для территории, ограниченной координатами: ![]() =
= ![]() ,
, ![]() =
= ![]()
Исходными данными для этой работы являлись карта средневзвешенных
значений плотностей осадочного чехла для территории СССР (Озерская М.Л.
и др., 1975) [6], которая учитывала осадочные толщи с мощностями в диапазоне
0 ![]() 5.9 км
(при ее построении были использованы данные по скважинам), и петроплотностная
карта геологических формаций СССР (Дортман Н,Б, и др., 1978) [7], использовавшаяся
для контроля реалистичности полученных теоретических зависимостей и для
установления сходства регионов по возрасту осадков и сходству условий осадконакопления.
5.9 км
(при ее построении были использованы данные по скважинам), и петроплотностная
карта геологических формаций СССР (Дортман Н,Б, и др., 1978) [7], использовавшаяся
для контроля реалистичности полученных теоретических зависимостей и для
установления сходства регионов по возрасту осадков и сходству условий осадконакопления.
Для тех регионов, где значения средневзвешенных плотностей
осадочного чехла ранее не оценивались, была разработана методика их оценки,
основанная на анализе регрессионных зависимостей средневзвешенной плотности
осадочных отложений ![]() от
их мощности
от
их мощности ![]() c учетом возрастания
плотности
c учетом возрастания
плотности ![]() с глубиной. Для
получения регрессионных зависимостей второго порядка
с глубиной. Для
получения регрессионных зависимостей второго порядка ![]() в
диапазоне мощностей осадков
в
диапазоне мощностей осадков ![]()
![]() км
использовались данные с карты М.Л.Озерской. Эти зависимости строились для
интервала значений
км
использовались данные с карты М.Л.Озерской. Эти зависимости строились для
интервала значений ![]()
![]() км,
так как в нем вероятностная зависимость
км,
так как в нем вероятностная зависимость ![]() близка
к квадратической, а при больших мощностях осадков к линейной.
близка
к квадратической, а при больших мощностях осадков к линейной.
Математическое выражение для регрессии второго порядка имеет вид:
Коэффициенты в (3) выражаются следующим образом:
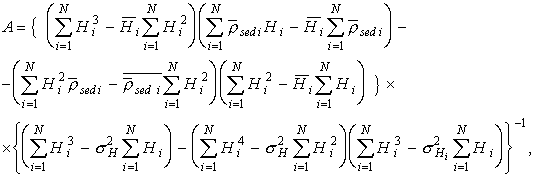
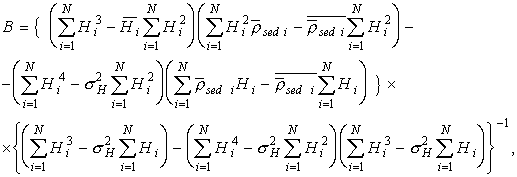
где 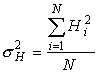 ,
, 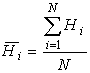 ,
, 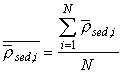 и
и ![]() -
число точек.
-
число точек.
На основании регрессионного анализа на изучаемой территории были выделены 10 эталонных участков:
1. Восточно-Европейская платформа,
2. Западно-Сибирская платформа,
3. Средне-Сибирское плоскогорье,
4. Средняя Азия,
5. Урал,
6. Кавказ,
7. Таймыр - Обская губа,
8. Байкал,
9. Вилюйская синеклиза,
10. Туранская плита.
Для каждого полигона были построены регрессионные зависимости
(3) для ![]() от
от ![]() мощности
осадочных отложений в диапазоне значений мощности осадков от 0 до 3.5 км.
мощности
осадочных отложений в диапазоне значений мощности осадков от 0 до 3.5 км.
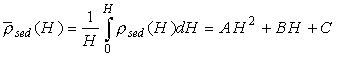 .
(4)
.
(4)При этом оказалось, что свободные члены регрессионных
зависимостей для всех полигонов равны значениям поверхностных плотностей ![]() указанным
на карте Н.Б.Дортман. Это обстоятельство убедило нас в том, что полученные
регрессионные зависимости удовлетворительны, так как
указанным
на карте Н.Б.Дортман. Это обстоятельство убедило нас в том, что полученные
регрессионные зависимости удовлетворительны, так как ![]()
Продифференцировав (4), получаем зависимость плотности
осадков ![]() от
глубины
от
глубины ![]() :
:
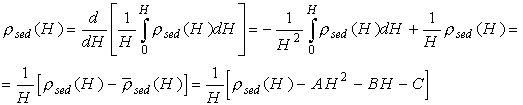
Отсюда имеем: ![]() .
(5)
.
(5)
Для осадочных толщ мощностью более 3.5 км зависимость
аппроксимировалась кусочно-непрерывной функцией, совпадающей с (5) при
мощности осадков менее 3.5 км, линейно-возрастающей в диапазоне мощностей
от 3.5 км до 7.5 км до значения 2.64 г/см3, а для больших глубин
значение ![]() принималось
постоянным и равным 2.64 г/см3. Если максимальное значение в
слое до 3.5 км (вершина параболы) достигалось на глубинах меньших 3.5 км
и было меньше 2.64 г/см3, то далее до границы слоя
принималось
постоянным и равным 2.64 г/см3. Если максимальное значение в
слое до 3.5 км (вершина параболы) достигалось на глубинах меньших 3.5 км
и было меньше 2.64 г/см3, то далее до границы слоя ![]() считалась
постоянной и равной этому максимальному значению. Если же максимальное
значение в слое до 3.5 км было больше или равно 2.64 г/см3,
то далее на всю оставшуюся мощность распространялось это максимальное значение
плотности. Эта зависимость осреднялась с соответствующими весами, т.е.
считалась
постоянной и равной этому максимальному значению. Если же максимальное
значение в слое до 3.5 км было больше или равно 2.64 г/см3,
то далее на всю оставшуюся мощность распространялось это максимальное значение
плотности. Эта зависимость осреднялась с соответствующими весами, т.е. ![]() вычислялась
по формулам:
вычислялась
по формулам:
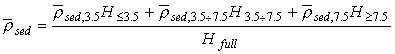 ,
,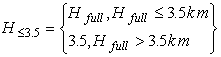 ,
(6)
,
(6)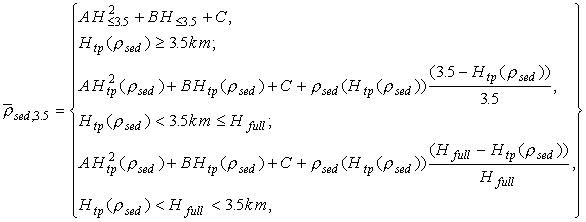 ,
,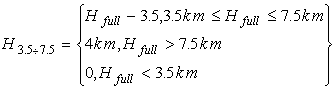 ,
,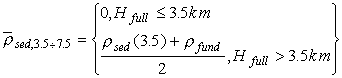 ,
,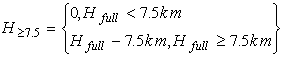 ,
,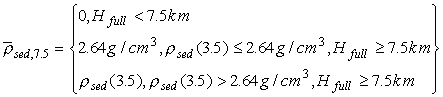 ,
(6)
,
(6)
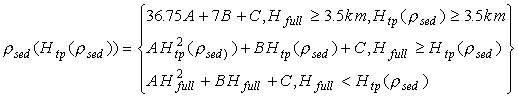 ,
,Для расчета эквирельефа Евразии все известные массы в верхней части земной коры (рельеф, осадки и вода) представлялись в виде однородной пластины с плотностью равной средней плотности коры, за которую в работе было принято значение 2.67 г/см3. "Конденсируя" воду и осадки до этой стандартной плотности, мы получили вместо поверхности "дневного" рельефа поверхность так называемого "приведенного" рельефа, характеризующего суммарную "нагрузку".
Значения высот (глубин) эквирельефа будут:
для суши ![]() ,
,
для моря ![]() ,
,
где ![]() -
высота (глубина) осредненного рельефа,
-
высота (глубина) осредненного рельефа, ![]() -
мощность осадочного слоя,
-
мощность осадочного слоя, ![]() -
средневзвешенная плотность осадков.
-
средневзвешенная плотность осадков.
Для Антарктиды у нас не было данных о мощностях и средних плотностях слагающих пород осадочных бассейнов, и поэтому при расчете эквирельефа учитывался только ледниковый покров.
Значения мощностей ледникового покрова высот рельефа ложа
ледника брались с карт, составленных И.А.Суетовой для готовящегося к изданию
Атласа Антарктиды [8]. Для льда бралось значение плотности ![]() г/см3.
г/см3.
Для расчета эквирельефа Антарктики все известные массы в верхней части земной коры (рельеф, лед и вода) представлялись в виде однородной пластины с плотностью равной средней плотности коры, за которую в работе было принято значение 2.67 г/см3. "Конденсируя" воду и осадки до этой стандартной плотности, мы получили вместо поверхности "дневного" рельефа поверхность так называемого эквирельефа, характеризующего суммарную "нагрузку".
Значения высот (глубин) эквирельефа будут:
для суши и промерзшего до дна моря ![]() ,
,
для моря при отсутствии льда ![]() ,
,
для моря, покрытого плавающим льдом (шельфовый ледник) ![]() ,
,
где ![]() -
высота (глубина) осредненного рельефа,
-
высота (глубина) осредненного рельефа, ![]() -
мощность ледникового покрова,
-
мощность ледникового покрова, ![]() -
плотность льда.
-
плотность льда.
Для дальнейшего использования в работе, которой посвящена данная статья, полученные таким образом высоты эквирельефа по сети 1Ох1О осреднялись, чтобы получить значения по сети 5Ох 5О.
В качестве исходных данных для оставшейся части Земли
были взяты значения высот и глубин по одноградусной сетке, представленные
нам Мировым центром данных РАН [9], осредненные нами по пятиградусной сетке.
При этом для получения высот эквирельефа данные по морским акваториям предварительно
приводились нами согласно (7). На рис.2 представлена
исходная карта высот эквивалентного рельефа Земли.
Разложение высот эквирельефа по сферическим функциям проводилось
по той же методике, что и для поверхности M (Мохоровичича) [10].
Полученные коэффициенты разложения по N=30 (![]() )
приведены в таблице 1. На рис.3
представлена кривая изменения среднеквадратической ошибки аппроксимации
исходных высот при увеличении степени разложения N:
)
приведены в таблице 1. На рис.3
представлена кривая изменения среднеквадратической ошибки аппроксимации
исходных высот при увеличении степени разложения N:
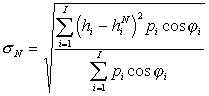 ,
,Видно, что основные черты эквирельефа в максимальной степени
отражаются в гармониках 1![]() 5 степени
(как и для поверхности Мохо). При N>5 ошибки аппроксимации убывают
более плавно, достигая 0.24 км при N=30 (при среднем разбросе исходных
высот относительно средней уровенной поверхности равном 1.52 км).
5 степени
(как и для поверхности Мохо). При N>5 ошибки аппроксимации убывают
более плавно, достигая 0.24 км при N=30 (при среднем разбросе исходных
высот относительно средней уровенной поверхности равном 1.52 км).
На рис. 4 приведена карта остаточных
разностей ![]() .
Видно, что в разложении данной степени N=30 не нашли отражение мелкие
неровности рельефа протяженностью
.
Видно, что в разложении данной степени N=30 не нашли отражение мелкие
неровности рельефа протяженностью ![]() км.
Максимальное значение невязок (
км.
Максимальное значение невязок (![]() 1.2
км) соответствуют высокогорным районам материков (Тибет, Восточная Антарктида)
и прибрежным зонам.
1.2
км) соответствуют высокогорным районам материков (Тибет, Восточная Антарктида)
и прибрежным зонам.
В целях сравнительного анализа поверхности эквирельефа и поверхности M мы определяли на основе таблицы 1 те же параметры, что для поверхности M , а именно:
1) средний радиус ![]() км;
км;
2) смещение геометрического центра относительно центра масс Земли:
![]() 0.66
км - смещение вдоль экваториальной оси, соответствующей
0.66
км - смещение вдоль экваториальной оси, соответствующей ![]() ;
;
![]() 0.41
км - смещение вдоль экваториальной оси, соответствующей
0.41
км - смещение вдоль экваториальной оси, соответствующей ![]() ;
;
![]() 0.70 км - смещение
вдоль северной полярной оси;
0.70 км - смещение
вдоль северной полярной оси;
![]() 1.05 км,
1.05 км, ![]() -
величина и координаты общего смещения ( к югу Европейской части России
);
-
величина и координаты общего смещения ( к югу Европейской части России
);
3) параметры эллипсоида наилучшего приближения:
![]() + 7.39 км,
+ 7.39 км, ![]() =
= ![]() ,
, ![]() -
величина и координаты большой экваториальной полуоси;
-
величина и координаты большой экваториальной полуоси;
![]() км,
км, ![]() ,
, ![]() -
величина и координаты малой экваториальной полуоси;
-
величина и координаты малой экваториальной полуоси;
![]() км,
км, ![]() ,
, ![]() -
величина и координаты полярной полуоси;
-
величина и координаты полярной полуоси;
![]() км
- средний экваториальный радиус;
км
- средний экваториальный радиус;
![]() -
полярное сжатие;
-
полярное сжатие;
![]() -
экваториальное сжатие;
-
экваториальное сжатие;
4) статистические характеристики:
![]() -
степенная дисперсия высот рельефа (рис.5, кривая
1);
-
степенная дисперсия высот рельефа (рис.5, кривая
1);
![]() ;
; 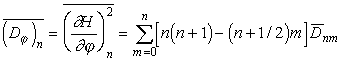 -
дисперсия изменения высот рельефа при движении вдоль меридианов (рис.5,
кривая 2:
-
дисперсия изменения высот рельефа при движении вдоль меридианов (рис.5,
кривая 2: ![]() );
);
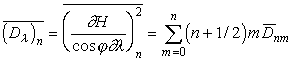 -
дисперсия изменения высот рельефа при движении вдоль параллелей (рис.5,
кривая 3:
-
дисперсия изменения высот рельефа при движении вдоль параллелей (рис.5,
кривая 3: ![]() );
);
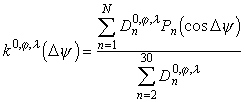 -
автоковариационная функция (рис.6).
-
автоковариационная функция (рис.6).
Анализ рис. 5, рис.6
подтверждает вывод о том, что основные черты эквирельефа отражаются в гармониках
1![]() 5 степени. При n>10
дисперсия падает на порядок по сравнению с дисперсией 1
5 степени. При n>10
дисперсия падает на порядок по сравнению с дисперсией 1![]() 5
степени и очень медленно убывает с ростом степени разложения. Заметна некоторая
неизотропность рельефа для гармоник 1
5
степени и очень медленно убывает с ростом степени разложения. Заметна некоторая
неизотропность рельефа для гармоник 1![]() 4
степени, обусловленная превалированием материков в северном полушарии (дисперсия
по широте) и наличием Тихого океана (дисперсия по долготе). При n>10
рельеф можно считать практически изотропным. Корреляция рельефа несущественна
(k<0.5) между точками, отстоящими на
4
степени, обусловленная превалированием материков в северном полушарии (дисперсия
по широте) и наличием Тихого океана (дисперсия по долготе). При n>10
рельеф можно считать практически изотропным. Корреляция рельефа несущественна
(k<0.5) между точками, отстоящими на ![]() >
>![]() .
.
Основное отличие от аналогичных графиков для поверхности
Мохоровичича обусловлено разным соотношением гармоник 2-ой и 4-ой степени
для этих поверхностей.
Если бы массы рельефа Земли целиком изостатически компенсировались на глубине поверхности М, то соотношение гармонических коэффициентов разложения глубин поверхности М и высот эквирельефа (относительно геоида ) подчинялось бы следующему соотношению:
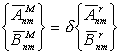 ,
где
,
где ![]() ;
;![]() г/см3 - средняя плотность масс рельефа;
г/см3 - средняя плотность масс рельефа; ![]() -
скачок плотности на границе Мохо.
-
скачок плотности на границе Мохо.
Однако сравнение таблиц гармонических коэффициентов для
поверхности М и рельефа показывает, что нет такой прямой зависимости
(таблица 2, ![]() ;
; ![]() ).
).
На рис.7 представлена зависимость
средневесовых для каждой степени коэффициентов ![]() от
степени гармоник:
от
степени гармоник:
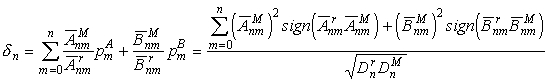 ,
,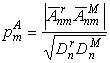 ,
, 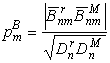 - порядковые веса коэффициентов
- порядковые веса коэффициентов В среднем, для всех n, кроме n = 1,2, ![]() и
убывает с увеличением n :
и
убывает с увеличением n : ![]()
![]()
![]()
Обычно принимается гипотеза зависимости изостатической компенсации от степени гармоники: более мелкие неровности рельефа, характеризующиеся гармониками более высокой степени, изостатически слабо или совсем не компенсируются. Для проверки этой гипотезы мы посчитали степенные коэффициенты взаимной корреляции двух поверхностей:
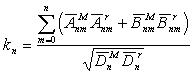 .
.Оптимальная (наилучшая) компенсация масс рельефа на поверхности M осуществляется при следующих значениях:
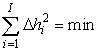 ).
).
По-видимому, в данных картах суммируется вклад некомпенсированного рельефа и аномальных плотностных зон коры, не учитываемых нами. Из анализа этих карт можно сделать некоторые выводы о возможном характере изостатической компенсации отдельных регионов Земли: Евразия, Австралия, Южная Америка в целом перекомпенсированы, Африка, Гренландия - недокомпенсированы; западная часть Тихого океана и южная Атлантика - недокомпенсированы; восток Тихого океана и северная Атлантика - перекомпенсированы (рис.9а, b). На рис.9с можно увидеть более мелкие некомпенсированные структуры. Детальный анализ этих карт можно сделать, сравнивая их с конкретными геологическими структурами. Можно также увидеть любопытную корреляцию карты некомпенсированного рельефа (n=5, рис.9a) c картой границы ядро-мантия, полученной по сейсмическим данным [12].
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.000006
|
|
1) геометрический центр поверхности M сдвинут почти
симметрично относительно центра поверхности эквирельефа, отклоняясь от
точки симметрии ![]() к
северо-западу на
к
северо-западу на ![]() . Поскольку
в высотах геоида отсутствуют гармоники первой степени, то, по-видимому,
нарушение симметрии в расположении поверхности М и рельефа компенсируется
на больших глубинах;
. Поскольку
в высотах геоида отсутствуют гармоники первой степени, то, по-видимому,
нарушение симметрии в расположении поверхности М и рельефа компенсируется
на больших глубинах;
2) направление большой и малой осей экваториального сечения
М также несколько отклоняется от соответствия теории компенсации
(сдвиг ![]() к востоку). Направление
аналогичных полуосей геоида обусловлено, в основном, поверхностью M
и, по-видимому, нижележащими слоями;
к востоку). Направление
аналогичных полуосей геоида обусловлено, в основном, поверхностью M
и, по-видимому, нижележащими слоями;
3) в то время, как полярное сжатие поверхности эквирельефа Земли меньше сжатия геоида и даже гидроэллипсоида, полярное сжатие поверхности М значительно превышает сжатие геоида и гидроэллипсоида. Таким образом, отличие сжатия геоида от сжатия гидроэллипсоида, обычно трактуемое как соответствие сжатия твердой оболочки Земли более быстрой в древности скорости вращения Земли, объясняется совершенно другой причиной: большим сжатием пластичной оболочки Земли. Причину такого большого сжатия, по-видимому, следует искать в более глубоких недрах Земли.
Из представленных на рис.10 графиков степенных коэффициентов взаимной корреляции поверхностей эквирельефа Мохо и геоида, построенных относительно гидростатического эллипсоида, можно сделать следующие выводы;
1) значительная положительная корреляция (k=0.73)
геоида и M для n=2 подтверждает вывод об обусловленности
избыточного сжатия геоида сжатием M (рис.10b).
Гармоники низкой степени ![]() гравитационного
поля Земли, по-видимому, обусловлены влиянием более глубоких, чем кора
и верхняя мантия, слоев Земли (рис.10a,b). Можно
отметить значимую постоянную корреляцию эквирельефа и геоида для гармоник
n
гравитационного
поля Земли, по-видимому, обусловлены влиянием более глубоких, чем кора
и верхняя мантия, слоев Земли (рис.10a,b). Можно
отметить значимую постоянную корреляцию эквирельефа и геоида для гармоник
n![]()
![]() ;
;
2) общепринятая практика интерполяции глубин Мохо на основе
аномалий Буге не подтверждается для всех степеней гармоник n![]() (см.рис.10c,
где из гравитационного поля удален гравитационный вклад эквирельефа:
(см.рис.10c,
где из гравитационного поля удален гравитационный вклад эквирельефа:
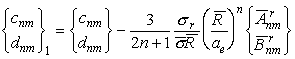 .
.3) коэффициенты ![]() общей
взаимной корреляции различных поверхностей для
общей
взаимной корреляции различных поверхностей для ![]() свидетельствуют
в пользу интерполяции глубин M на основе гипотезы изостатической
компенсации рельефа:
свидетельствуют
в пользу интерполяции глубин M на основе гипотезы изостатической
компенсации рельефа:
|
|
|
|
|
|
|
|
|
|
|
|
1. G. Balmino, K. Lambeck, W. Kaula. A spherical harmonic analysis of the Earth's topography // J.Geophys. Res., 1973, 78, N 2,478-481.
2. А.М. Щербаков. Гармонический анализ рельефа Земли по сферическим функциям до 30-30 порядка и степени // Физика Земли, 1983, №11, 15-27.
3. Структурная карта поверхности фундамента платформенных территорий СССР, М 1:500 000, Гл. ред. В.В.Семенович, Я.И.Ровнин, Н.В.Неволин, И.Ю.Зайченко и др., МинГео СССР, МинГео РСФСР,1982.
4. Тектоническая карта дальневосточных морей и сопредельных территорий, M 1:2 500 000, Ред.-сост. В.В.Харакинов, Главморнефтегаз, ВПО Сахалинморнефтегазпром, отчет от 2.07.1984.
5. Тектоническая карта. Охотоморский регион, М 1:1 500 000, сост. В.В. Харахинов, В.А.Бабошина, А.А.Терещенкова, Главморнефтегаз, ВПО Сахалинморнефтегазпром, Сахалин НИПИнефтегаз, отчет №1-84-39кш/5.
6. Карта рельефа поверхности фундамента Евразии, М 1:15 000 000, Гл.ред. В.В.Белоусов, Зам. гл. ред. Н.Я.Кунин, В.Б.Мазур, Б.К.Остистый, М.И.Островский, ИФЗ АН СССР, МинГео СССР,1987.
7. Дортман Н.Б., Дубинчик Е.Я., Зотова И.Ф. Плотностная
карта геологических формаций территории СССР, Москва, Мингео,
М 1: 10 000 000, 1978.
8. Атлас Антарктиды (в печати).
9. 1 - degree gridded elevations/bathymetry for the world by Scripps Institution of Oceanography (S10) // Russian Academy of Sciences, World Data Center B for Solid Earth Physics.
10. Н.А.Чуйкова, Т.Г.Максимова. Гармонический и статистический анализ глубин поверхности Мохоровичича //Труды ГАИШ, том 65, стр. 33-50.
11. Dziewonski, Anderson, Preliminary reference Earth model // Physics of the Earth and Planetary interiors, 25 : 297-356.
12. Morelli, Dziewonski. Topography of the core-mantle boundary and lateral homogeneity of the liquid core // Nature, vol. 325, 1987, p.678.