Резюме. Получены дифференциальные уравнения модельной задачи о движении внутреннего ядра Земли (однородного шара) в жидком ядре в поле несферичной неоднородной мантии и с учетом притяжения Луны и Солнца. В результате упрощений эти уравнения сведены к системе трех линейных дифференциальных уравнений второго порядка с условно-периодическими коэффициентами. Для различных моделей взаимодействия с жидким ядром определены частоты собственных колебаний твердого ядра. Изучен эффект постоянного смещения центра масс внутреннего ядра вследствие гравитационного влияния неоднородностей на границе ядро-мантия. Получены оценки амплитуды вынужденных колебаний ядра вследствие сезонного перераспределения масс Земли. Выявлены вековые эффекты в его движении следствии изменения уровня мирового океана, ледовых покровов Антарктиды и Гренландии, а также вследствие субдукции и аккумуляции масс океанических плит.
В данной работе изучаются движения твердого ядра Земли
на основе сравнительно простой модельной задачи. Будем рассматривать движение
системы трех тел: Земля-Луна-Солнце, в которой Луна и Солнце рассматриваются
как материальные точки с массами ![]() и
и ![]() ,
а Земля как составное тело.
,
а Земля как составное тело.
Модель Земли состоит из внутреннего твердого ядра ![]() ,
внешнего жидкого ядра
,
внешнего жидкого ядра ![]() и
мантии
и
мантии ![]() .
Внутреннее ядро в данной работе будет рассматриваться как шар (однородный
или с концентрическим распределением плотностей) с пренебрежимо малой массой.
Внешнее ядро представляет собой идеальную несжимаемую однородную жидкость,
заполняющую полностью мантийную полость. В общем случае поверхность внешнего
ядра является несферической. Мантия
.
Внутреннее ядро в данной работе будет рассматриваться как шар (однородный
или с концентрическим распределением плотностей) с пренебрежимо малой массой.
Внешнее ядро представляет собой идеальную несжимаемую однородную жидкость,
заполняющую полностью мантийную полость. В общем случае поверхность внешнего
ядра является несферической. Мантия ![]() рассматривается
как несферическая неоднородная неизменяемая оболочка.
рассматривается
как несферическая неоднородная неизменяемая оболочка.
Наша цель - изучить движение твердого ядра ![]() с
учетом гидродинамического и гравитационного влияния жидкого ядра
с
учетом гидродинамического и гравитационного влияния жидкого ядра ![]() ,
а также с учетом гравитационного притяжения внешней оболочки (мантии
,
а также с учетом гравитационного притяжения внешней оболочки (мантии ![]() ),
Луны и Солнца.
),
Луны и Солнца.
Постановка задачи имеет ограниченный характер. Предполагается,
что мантийная оболочка вращается вместе с жидким ядром как одно твердое
(неизменяемое) тело относительно главной центральной полярной оси инерции,
сохраняющей ориентацию в пространстве, с постоянной угловой скоростью ![]() .
Т.е. здесь не учитываются тонкие особенности вращения Земли, такие как
прецессия, нутация и движение ее полюсов, не рассматриваются течения в
жидком ядре.
.
Т.е. здесь не учитываются тонкие особенности вращения Земли, такие как
прецессия, нутация и движение ее полюсов, не рассматриваются течения в
жидком ядре.
Формально считаем, что ядро ![]() имеет
малые размеры и массу, т.е. как его притяжение, так и смещения не влияют
на вращение внешней оболочки. Само же твердое ядро совершает движение в
жидком ядре, испытывая его гидростатическое влияние, под действием всех
составных частей Земли, а также внешних небесных тел: Луны и Солнца. Предполагаем,
что относительно барицентра системы Земля-Луна-Солнце каждое из тел совершает
орбитальное движение в соответствии с их современными аналитическими теориями.
имеет
малые размеры и массу, т.е. как его притяжение, так и смещения не влияют
на вращение внешней оболочки. Само же твердое ядро совершает движение в
жидком ядре, испытывая его гидростатическое влияние, под действием всех
составных частей Земли, а также внешних небесных тел: Луны и Солнца. Предполагаем,
что относительно барицентра системы Земля-Луна-Солнце каждое из тел совершает
орбитальное движение в соответствии с их современными аналитическими теориями.
Cxyz - основная система координат, оси которой
направлены по главным центральным осям инерции системы внешнее ядро-мантия.
При сделанных предположениях эти оси оказываются жестко связанными с мантией ![]() .
.
Таким образом, для принятой модели C - центр масс Земли. Полярная ось инерции Cz совпадает с осью вращения и сохраняет фиксированное направление в пространстве. Вместо главных центральных осей инерции Cxyz в качестве основной системы координат также может использоваться гринвичская земная система координат.
Внешними возмущающими телами являются Луна и Солнце. Их
положение в земной системе координат Cxyz зададим сферическими координатами ![]() и
и ![]() ;
соответственно r - расстояние от центра масс Земли C до возмущающего
тела,
;
соответственно r - расстояние от центра масс Земли C до возмущающего
тела, ![]() - широта,
- широта, ![]() - долгота. Эти тела совершают известные движения, и координаты
- долгота. Эти тела совершают известные движения, и координаты ![]() представляются
известными функциями времени в виде рядов Фурье или Пуассона.
представляются
известными функциями времени в виде рядов Фурье или Пуассона.
Введем также барицентрическую систему координат (для системы Земля-Луна-Солнце) BXYZ с началом в барицентре этой системы тел, оси которой сохраняют фиксированные направления в пространстве (при этом ось BZ направлена параллельно оси вращения Земли Cz).
Цель данной работы - получить дифференциальные уравнения движения твердого ядра в неинерциальной системе отсчета Cxyz с учетом воздействий на него со стороны жидкого ядра, несферичной мантии, а также со стороны Луны и Солнца. Оценить порядок и значимость каждого из указанных возмущающих факторов. Выполнить предварительные исследования основных динамических эффектов в движении твердого ядра.
Для численных оценок будем использовать параметры динамического строения Земли по модели Дзевонского-Андерсона PREM [1]. Поверхность внешнего ядра Земли будем задавать уравнением Дзевонского-Морелли [2].
Введем в рассмотрение следующие параметры:
![]() -
средняя плотность внутреннего ядера Земли;
-
средняя плотность внутреннего ядера Земли; ![]() плотность
жидкого ядра вблизи поверхности внутреннего ядра;
плотность
жидкого ядра вблизи поверхности внутреннего ядра; ![]() -
средние радиусы внутреннего ядра и внешнего ядра;
-
средние радиусы внутреннего ядра и внешнего ядра; ![]() -массы
внутреннего и внешнего ядер,
-массы
внутреннего и внешнего ядер, ![]()
![]()
![]() -
массы мантии и всей Земли;
-
массы мантии и всей Земли; ![]() -
средний радиус Земли.
-
средний радиус Земли.
Основные частоты задачи ![]() определим
формулами
определим
формулами
где f - гравитационная постоянная, а соответствующие им периоды
Численные значения указанных здесь параметров составляют:
2.I. Сила взаимодействия с жидким ядром.
Описание силового взаимодействия твердого ядра с жидким
ядром представляет собой сложную гидродинамическую задачу. Поэтому в первых
исследованиях по динамике твердого ядра для силы ![]() ,
действующей на него со стороны жидкого ядра, принимались наиболее простые
выражения (см., например, [ 3 ], [ 4 ], [5]).
,
действующей на него со стороны жидкого ядра, принимались наиболее простые
выражения (см., например, [ 3 ], [ 4 ], [5]).
В первом приближении, по-видимому, вполне естественно
допустить, что эта сила, учитывающая гидростатическое и гравитационное
взаимодействие с жидким ядром, является центральной и описывается формулой ![]() (1)
(1)
где ![]() - некоторый постоянный коэффициент, учитывающий особенности взаимодействия
внешнего и внутреннего ядра,
- некоторый постоянный коэффициент, учитывающий особенности взаимодействия
внешнего и внутреннего ядра, ![]() -
радиус-вектор центра инерции
-
радиус-вектор центра инерции ![]() твердого
ядра в основной системе координат Cxyz, (x,y,z)
- декартовы координаты точки
твердого
ядра в основной системе координат Cxyz, (x,y,z)
- декартовы координаты точки ![]() .
.
В первых работах по динамике внутреннего ядра для коэффициента ![]() принималось наиболее простое выражение:
принималось наиболее простое выражение:
Сила (1), (2) представляет собой совокупность ньютоновской
силы тяготения и выталкивающей силы гидростатического давления, действующих
на твердое ядро со стороны жидкого ядра. При этом "вытесненная жидкость"
считается однородной с плотностью ![]() ,
а внутреннее ядро обладает концентрическим распределением плотностей (со
средней плотностью
,
а внутреннее ядро обладает концентрическим распределением плотностей (со
средней плотностью ![]() ).
).
Если формально учесть, что "вытесненная жидкость" не является
однородной, а в квазистатическом приближении сохраняется ее концентрический
характер, то для коэффициента ![]() в (1) получаем выражение
в (1) получаем выражение ![]()
![]() (3)
(3)
где ![]() -
масса внутреннего ядра, но вычисленная для закона распределения плотностей,
установленного моделью Земли PREM [1] для жидкого ядра.
-
масса внутреннего ядра, но вычисленная для закона распределения плотностей,
установленного моделью Земли PREM [1] для жидкого ядра.
В качестве альтернативного метода также была определена гидростатическая сила, действующая на смещенное сферическое внутреннее ядро со стороны жидкого ядра. Допускается, что в квазистатическом приближении сохраняется концентричность в распределении плотностей и давлений в жидком ядре. В этом упрощенном варианте для центральной силы (1)
Здесь ![]() значение
градиента давления на подошве внешнего ядра. В соответствии с моделью Земли
PREM примем
значение
градиента давления на подошве внешнего ядра. В соответствии с моделью Земли
PREM примем
Для базовых параметров задачи, приведенных в п.1 и для значения градиента (5), и для указанных выше трех вариантов представления центральной силы (1)-(4) имеем следующие значения коэффициентов:
Более близкими к реальности, по-видимому, являются значения ![]() ,
хотя обоснование этого положения должно опираться на углубленный гидродинамический
анализ движения твердого ядра в жидком ядре с учетом других их реальных
особенностей.
,
хотя обоснование этого положения должно опираться на углубленный гидродинамический
анализ движения твердого ядра в жидком ядре с учетом других их реальных
особенностей.
Ясно, что параметр ![]() определяется неуверенно. Поэтому для оценок соответствующих динамических
эффектов в движении твердого ядра целесообразно варьировать его значения.
По этой причине ниже мы даем подобные оценки для всех значений параметров
(6).
определяется неуверенно. Поэтому для оценок соответствующих динамических
эффектов в движении твердого ядра целесообразно варьировать его значения.
По этой причине ниже мы даем подобные оценки для всех значений параметров
(6).
Силовая функция, соответствующая силе (1), определяется
формулами ![]() (7)
(7)
При более точных постановках задачи эта силовая функция
будет также содержать линейные и смешанные члены.
Компоненты соответствующей силы притяжения выражаются
через частные производные по координатам следующей силовой функции [6]: 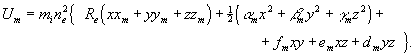 (8)
(8)
Здесь ![]()
![]()
![]() (9)
(9)
![]()
![]() em = 3Em,
em = 3Em, ![]()
безразмерные коэффициенты, определяемые с помощью следующих объемных интегралов:
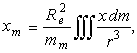
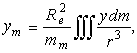
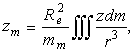 (10)
(10)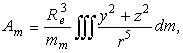
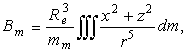
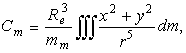
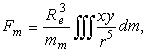
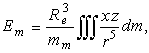
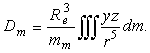 (11)
(11)В (10), (11) x,y,z - координаты текущей точки мантии, ![]() -
элементарная масса,
-
элементарная масса, ![]() -
плотность в этой точке. Интегрирование распространено на весь объем мантии.
-
плотность в этой точке. Интегрирование распространено на весь объем мантии.
Интегралы в (10), (11) определяют величины, аналогичные
координатам центра масс, осевым и центробежным моментам инерции, но для
тела с другими законами распределения плотностей ![]() .
.
Формула (8), (9) в общем случае является приближенной
(в разложении силовой функции сохранены лишь первая и вторая гармоники).
Однако, существует класс тел, для которых эта формула является точной.
К подобным телам относятся однородные оболочки, внешние и внутренние поверхности
которых представляют собой произвольные эллипсоиды.
Объемные интегралы в (10),(11) фактически определяют значения компонент силы ньютоновского притяжения несферичной оболочки в точке С, т.е. в центре масс:
Для определенных тел эти интегралы обращаются в нуль. Например, если оболочка обладает тремя взаимно-ортогональными плоскостями динамической симметрии. Однако, в общем случае эти интегралы имеют ненулевые значения.
Возникает важная задача по определению координат такой точки, для которой все три компоненты силы (12) равны нулю. Покажем, что такая точка существует для широкого класса тел с почти-концентрическим распределением плотностей. В дальнейшем будем называть эту точку гравитационным центром и обозначим его G.
Для определения декартовых координат этого центра ![]() в
системе координат Cxyz получаем систему трех уравнений:
в
системе координат Cxyz получаем систему трех уравнений:
Если координаты ![]() малы,
что имеет место, например, если тело
малы,
что имеет место, например, если тело ![]() достаточно
близко по динамическому строению к телу с тремя взаимно ортогональными
плоскостями динамической симметрии, то они в первом приближении определяются
системой линейных алгебраических уравнений:
достаточно
близко по динамическому строению к телу с тремя взаимно ортогональными
плоскостями динамической симметрии, то они в первом приближении определяются
системой линейных алгебраических уравнений:
(коэффициенты и свободные члены этих уравнений определяются формулами (9)-(11)). Решение уравнений (14) существует при условии:
Высшие приближения координат гравитационного центра определяются
последовательностью алгебраических уравнений линейных и неоднородных аналогичных
системе (14).
Величины (11) аналогичны компонентам тензора инерции,
но вычислены для другого закона распределения плотностей этого же тела
(плотность делится на ![]() ).
Компоненты этого нового тензора позволяют также определить некоторые главные
оси по отношению к системе координат Gxyz с началом в гравитационном
центре G и с осями, параллельными основной системе координат Cxyz.
Указанные главные оси обозначим
).
Компоненты этого нового тензора позволяют также определить некоторые главные
оси по отношению к системе координат Gxyz с началом в гравитационном
центре G и с осями, параллельными основной системе координат Cxyz.
Указанные главные оси обозначим ![]() .
Очевидно, что они могут совпасть с осями системы координат Gxyz
только в специальных случаях, например, когда оболочка обладает тремя взаимно-ортогональными
плоскостями динамической симметрии. Оси координат
.
Очевидно, что они могут совпасть с осями системы координат Gxyz
только в специальных случаях, например, когда оболочка обладает тремя взаимно-ортогональными
плоскостями динамической симметрии. Оси координат ![]() можно
назвать главными центральными осями внутреннего потенциала оболочки Pm
(или его второй гармоники). Их определение и изучение представляет собой
важную задачу.
можно
назвать главными центральными осями внутреннего потенциала оболочки Pm
(или его второй гармоники). Их определение и изучение представляет собой
важную задачу.
Наряду с безразмерными параметрами (9) будем также использовать
параметры внутреннего потенциала, для которых здесь сохраним те же обозначения ![]() ,
как и для внешнего потенциала. Определим их формулами:
,
как и для внешнего потенциала. Определим их формулами:
Параметры (15) могут быть оценены для различных моделей несферичных оболочек Земли. Например, задаваемых системой материальных точек и др. Может эффективно использоваться модель тонких сферических однородных оболочек, охватывающих несферичные границы раздела сред (на границе ядро-мантия, литосфера-нижняя мантия и др.). Неоднородности в этом случае определяются особенностями поверхности раздела и контрастом (скачком) плотностей на ней.
2.2.3. Параметры гравитационного поля жидкого ядра. Смещение его центра масс .
Модель поверхности внешнего ядра Дзевонского-Морелли задает модуль радиус-вектора текущей точки поверхности в виде стандартного ряда по сферическим функциям долготы и широты этой текущей точки. По значениям коэффициентов этого ряда нетрудно определить коэффициенты стандартного представления внешнего гравитационного поля жидкого ядра, а также аналогичные коэффициенты внутреннего гравитационного потенциала тонкой оболочки, включающей в себя неоднородности на границе ядро-мантия.
Так, коэффициенты первой и второй гармоник внешнего потенциала несферичного жидкого ядра для его стандартного представления равны :
Эти значения были получены для значения плотности жидкого
ядра вблизи его поверхности ![]() г/см3.
Средний радиус ядра принимался
г/см3.
Средний радиус ядра принимался ![]() =3480
км. Хотя и со значительными погрешностями,
параметры (16) позволяют определить смещение центра масс жидкого ядра.
Так, в системе координат Cxyz координаты его центра масс равны:
=3480
км. Хотя и со значительными погрешностями,
параметры (16) позволяют определить смещение центра масс жидкого ядра.
Так, в системе координат Cxyz координаты его центра масс равны:
![]() (63
± 180) м,
(63
± 180) м, ![]() (-27
± 198) м,
(-27
± 198) м, ![]() (307
± 226) м,
(307
± 226) м,
Т.е. смещение центра масс жидкого ядра имеет место в направлении,
задаваемом координатами (в гринвичской системе координат) ![]() 77.4O
,
77.4O
,![]() -23.3O
и составляет 315 м .
-23.3O
и составляет 315 м .
Стоит заметить, что это смещение направлено в район Северной Атлантики, в котором находится ярко выраженное поднятие поверхности геоида (+60 м). С противоположной стороны Земли в районе Антарктиды находится участок с понижением уровня геоида (-60 м).
Указанные особенности геоида можно интерпретировать как
отражение глобального смещения внешнего ядра (или соответствующей этому
перестройке внешней оболочки) в сторону Северной Атлантики на 300![]() 400
м.
400
м.
2.2.4. Гравитационный центр неоднородностей на границе ядро-мантия.
В качестве примера оболочки рассмотрим тонкий шаровой слой Земли (с толщиной порядка 10 км), охватывающей неоднородности на границе ядро-мантия. Их происхождение связано с неправильностями поверхности внешнего ядра и большим скачком плотностей на этой границе 0.5973 г/см .
Силовая функция ньютоновского притяжения этими неоднородностями внутренних точек полости мантии определяется приближенной формулой (8), в которой согласно модели поверхности ядра [2], коэффициенты (9) имеют следующие численные значения:
Покажем, что этот гравитационный центр вполне вероятно совпадает с магнитным центром Земли. Последний, как известно, смещен на расстояние 436 км относительно геоцентра в направлении географической точки с координатами 15.410 с.ш., 1500 в.д.
Предположим, что гравитационный центр неоднородностей
совпадает с магнитным центром Земли, т.е. имеет следующие координаты ![]() ,
и по известным значениям коэффициентов второй гармоники из (17) найдем
значения:
,
и по известным значениям коэффициентов второй гармоники из (17) найдем
значения:
Эти значения в пределах погрешностей согласуются с их значениями из (17), полученными по данным наблюдений, а это свидетельствует о совпадении гравитационного центра неоднородностей на границе ядро-мантия и магнитного центра Земли.
В случае дальнейшего подтверждения этот факт может сыграть исключительно важную роль для гидродинамической интерпретации как механизма генерации магнитного поля Земли, так и для его эволюции, временных вариаций и инверсий. Последние могут быть вызваны изменениями положения магнитного (гравитационного) центра вследствие медленных изменений поверхности внешнего ядра.
По всей видимости, гравитационное и механическое воздействия неоднородностей на границе ядро-мантия являются управляющими структурой течений в жидком ядре и движением твердого ядра. Их взаимосвязанные движения в условиях воздействия других оболочек Земли, Луны и Солнца порождают наблюдаемое магнитное поле. Изучение гравитационных взаимодействий несферичных оболочек Земли , их глобальных относительных движений представляет собой основную задачу геодинамики.
Коэффициенты, аналогичные (17), но для стандартного представления внутреннего гравитационного потенциала тонкой шаровой оболочки, охватывающей неоднородности на границе ядро-мантия [2], в виде ряда по сферическим функциям, имеют следующие значения:
![]() (0.10 ± 0.16).10-4,
(0.10 ± 0.16).10-4, ![]() (0.37
± 0.13).10-4,
(0.37
± 0.13).10-4, ![]() (-0.69
± 0.16).10-4,
(-0.69
± 0.16).10-4,
![]() (0.20 ± 0.14).10-4,
(0.20 ± 0.14).10-4, ![]() (0.00
± 0.14).10-4
(18)
(0.00
± 0.14).10-4
(18)
Пусть имеется возмущающее тело ![]() (Луна
или Солнце) с массой
(Луна
или Солнце) с массой ![]() ,
положение которого в декартовой системе координат Cxyz задается
координатами
,
положение которого в декартовой системе координат Cxyz задается
координатами ![]() . По условию
эти координаты являются известными функциями времени.
. По условию
эти координаты являются известными функциями времени.
Силовая функция ньютоновского взаимодействия ядра и тела определяется формулой:
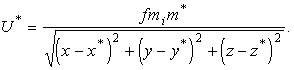
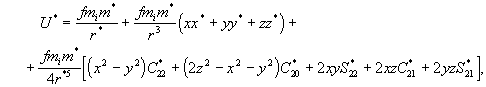
где ![]() -
простые функции координат возмущающего тела.
-
простые функции координат возмущающего тела.
Если ввести сферические координаты ![]() возмущающего
тела в осях Cxyz по формулам
возмущающего
тела в осях Cxyz по формулам
то функции ![]() можно
записать в следующем виде:
можно
записать в следующем виде:
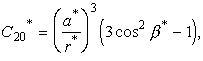 (19)
(19)
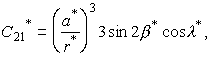
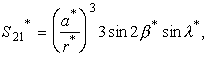
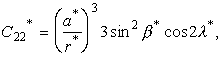
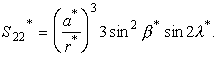
Для краткости мы опустим явные выражения этих рядов и
укажем лишь на их структуру. Для этого силовую функцию ![]() запишем
в более удобном виде:
запишем
в более удобном виде:
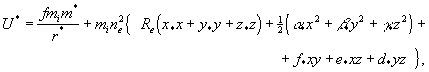 (20)
(20)![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() (21)
(21)
![]()
![]()
![]()
Возмущающими телами в нашей задаче являются Луна и Солнце.
Для этих тел коэффициенты ![]() (21)
представляются рядами вида:
(21)
представляются рядами вида:
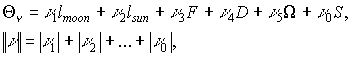 (23)
(23)где ![]() -
численные коэффициенты;
-
численные коэффициенты; ![]() -
определенные наборы целочисленных коэффициентов в аргументах
-
определенные наборы целочисленных коэффициентов в аргументах ![]() ;
; ![]()
![]()
![]() и
и ![]() -
соответствующие переменные Делоне Луны и Солнца из теорий их орбитальных
движений, которые являются определенными линейными функциями времени,
-
соответствующие переменные Делоне Луны и Солнца из теорий их орбитальных
движений, которые являются определенными линейными функциями времени, ![]() -
угол вращения Земли.
-
угол вращения Земли.
Ниже мы покажем, что в линейные члены силовой функции
(20),(21) не дают вклада в уравнения движения твердого ядра. Т.е. основные
возмущающие слагаемые в уравнениях движения будут линейными относительно
координат (x,y,z). При этом амплитуды возмущений будут определяться
параметром ![]() (численные значения
этого параметра для Луны и Солнца составляют
(численные значения
этого параметра для Луны и Солнца составляют ![]() =
0.25.10-7,
=
0.25.10-7,![]() =
0.12.10-7).
=
0.12.10-7).
Здесь мы ограничимся рассмотрением лишь указанных выше сил. Но заметим, что их список может быть значительно расширен. Дополнительные силы и возмущающие факторы учитывают реальные свойства гидродинамических взаимодействий (вязкость, сжимаемость, неоднородность жидкого ядра), электромагнитные взаимодействия, изменяемость во времени гравитационного поля оболочки и др.
Для компонент векторов, входящих в уравнение (24), введем
обозначения: ![]()
![]()
![]()
![]() Тогда
в проекциях на оси декартовой системы координат Cxyz уравнение (24) запишется
следующим образом:
Тогда
в проекциях на оси декартовой системы координат Cxyz уравнение (24) запишется
следующим образом:
Здесь ![]() -
проекции ускорения
-
проекции ускорения ![]() на
оси подвижной системы координат Cxyz.
на
оси подвижной системы координат Cxyz.
Силовая функция задачи объединяет все силовые функции,
рассмотренные выше в п.2 : ![]() где
где ![]() -
силовая функция центральной силы, учитывающей эффект гидростатического
отталкивания и гравитационного притяжения жидкого ядра (7);
-
силовая функция центральной силы, учитывающей эффект гидростатического
отталкивания и гравитационного притяжения жидкого ядра (7); ![]() -
силовая функция ньютоновского притяжения несферичной неоднородной мантии
(8) - (11);
-
силовая функция ньютоновского притяжения несферичной неоднородной мантии
(8) - (11); ![]() -
силовые функции ньютоновского притяжения твердого ядра Луной и Солнцем
(20) - (23).
-
силовые функции ньютоновского притяжения твердого ядра Луной и Солнцем
(20) - (23).
Каждая из указанных силовых функций (в принятом здесь приближении) имеет схожую структуру, а именно, содержит лишь линейные и квадратичные члены относительно координат. Поэтому
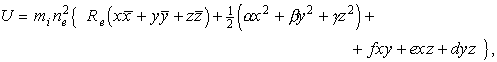 (26)
(26)Для определения компонент ускорения ![]() в
барицентрической системе координат Bxyz достаточно рассмотреть модель
системы Земля-Луна-Солнце в виде материальных точек с массами
в
барицентрической системе координат Bxyz достаточно рассмотреть модель
системы Земля-Луна-Солнце в виде материальных точек с массами ![]() .
При этом нетрудно показать, что слагаемые в правых частях уравнений (25)
от первых гармоник силовых функций Луны и Солнца взаимно сокращаются с
аналогичными слагаемыми, содержащими компоненты абсолютного ускорения .
.
При этом нетрудно показать, что слагаемые в правых частях уравнений (25)
от первых гармоник силовых функций Луны и Солнца взаимно сокращаются с
аналогичными слагаемыми, содержащими компоненты абсолютного ускорения .
Следовательно, уравнения движения твердого ядра в проекциях на подвижные оси системы координат (25) принимают следующий вид:
Весьма актуальными являются построения выражений силы ![]() для
гравитирующих твердого и внешнего ядер с учетом реальных особенностей их
формы и строения, стратификации, с учетом различных внешних массовых сил,
неинерциальности земной системы координат и др. В достаточно общем случае
выражение силы
для
гравитирующих твердого и внешнего ядер с учетом реальных особенностей их
формы и строения, стратификации, с учетом различных внешних массовых сил,
неинерциальности земной системы координат и др. В достаточно общем случае
выражение силы ![]() может
быть представлено формулой
может
быть представлено формулой ![]() ,
где
,
где ![]() ,
, ![]() ,
, ![]() -
относительное, переносное и кориолисово ускорения центра твердого ядра
в системе координат Cxyz,
-
относительное, переносное и кориолисово ускорения центра твердого ядра
в системе координат Cxyz, ![]() -
присоединенные массы твердого ядра (в общем случае они являются тензорными
характеристиками).
-
присоединенные массы твердого ядра (в общем случае они являются тензорными
характеристиками).
В данной работе примем предельно упрощенную трактовку
эффекта присоединенных масс. А именно, предположим, что ![]() [4].
Такой подход к проблеме оправдан в случае медленного вращения жидкого ядра
и при его достаточно малых размерах в первую очередь для изучения движений
твердого ядра, близких к полярным. При этом мы исходим из того факта, что
основные параметры модели (например,(2)) определяются весьма неуверенно.
[4].
Такой подход к проблеме оправдан в случае медленного вращения жидкого ядра
и при его достаточно малых размерах в первую очередь для изучения движений
твердого ядра, близких к полярным. При этом мы исходим из того факта, что
основные параметры модели (например,(2)) определяются весьма неуверенно.
С учетом сделанного предположения уравнения (28) можно записать в виде следующей системы линейных неоднородных дифференциальных уравнений шестого порядка (в общем случае с условно-периодическими коэффициентами вида (22), (23)):
![]() (29)
(29)
Напомним, что уравнения (29) получены при целом ряде упрощающих предположений. Тем не менее они пригодны для изучения движений ядра в малой окрестности геоцентра под действием сил, описанных выше .
Уравнения (29) являются интегрируемыми, а их общее решение
при произвольных начальных условиях ![]()
![]()
![]() ,
, ![]() ,
, ![]() ,
, ![]() (при
t=0) может быть представлено квадратурами или построено каким-либо
приближенным методом .
(при
t=0) может быть представлено квадратурами или построено каким-либо
приближенным методом .
В данной работе мы ограничимся предварительным анализом
уравнений (29) и анализом некоторых из основных динамических эффектов,
описываемых ими.
![]() (30)
(30)
![]()
Постоянное смещение ядра определяется частным решением
уравнений (30): ![]()
![]()
![]() ,
где
,
где ![]() - постоянные значения
координат, определяемые матричным уравнением:
- постоянные значения
координат, определяемые матричным уравнением:
(31)
Решение уравнения (31) определяется известными формулами.
Для наглядности можно также привести формулы приближенного
решения, которое легко строится методом последовательных приближений в
виде рядов: ![]()
![]()
![]() .
При этом основной эффект определяется формулами:
.
При этом основной эффект определяется формулами:
а дополнительные смещения ядра (эффекты второго порядка) определяются формулами:
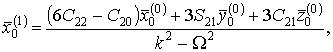
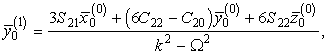
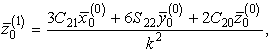 и т.д.
и т.д.
e) p) a)
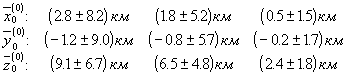 (33)
(33)
Расчетные значения координат (33) указывают, что ,вероятно, твердое ядро испытывает значительное смещение на расстояние 5 -15 км относительно геоцентра в направлении географической точки с координатами 25о з.д., 75о с.ш., т.е. примерно в направлении смещения центра масс жидкого ядра ( см. п. 2.2.3 ).
Общее решение однородных уравнений, соответствующих системе (30), имеет вид:
где ![]() -
произвольные постоянные интегрирования; коэффициенты
-
произвольные постоянные интегрирования; коэффициенты![]() и характеристические числа
и характеристические числа ![]() определяются
в результате решения известной системы однородных линейных алгебраических
уравнений.
определяются
в результате решения известной системы однородных линейных алгебраических
уравнений.
Величины ![]() определяются
как корни характеристического уравнения:
определяются
как корни характеристического уравнения:
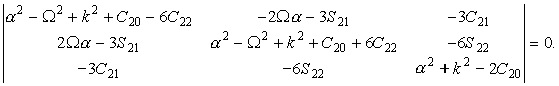 (35)
(35)Если пренебречь малыми значениями коэффициентов Cnm, Snm, то уравнение (35) упростится и его мнимые корни будут
Это означает, что решение (34) описывает собственные колебания твердого ядра с периодами, близкими по значениям к трем следующим:
Численные значения этих периодов для трех значений основного параметра задачи (6) составляют:
Вынужденные колебания ядра обуславливаются притяжением внешних небесных тел (Луны и Солнца), возмущениями в суточном вращении Земли и в движении ее полюсов, подвижными и изменяемыми массами в теле Земли и др.
Из-за ограниченного объема работы здесь мы не будем подробно
рассматривать вынужденные движения твердого ядра вследствие притяжения
Луны и Солнца, но приведем грубую оценку амплитуд возможных периодических
колебаний ядра с частотами ![]() .
.
Амплитуды этих возмущений первого порядка пропорциональны
величинам ![]() и
и ![]() ,
где
,
где ![]() - начальные значения
координат центра масс ядра,
- начальные значения
координат центра масс ядра, ![]() -
линейные комбинации частот задачи, соответствующих аргументам из формул
(22), (23).
-
линейные комбинации частот задачи, соответствующих аргументам из формул
(22), (23).
Оценки показали, что амплитуды вынужденных колебаний ядра
из-за притяжения Луны и Солнца могут достигать десятков сантиметров.
Метеорологические процессы со своим характерным периодом в среднем равным одному году являются, как известно, одной из основных причин вынужденных колебаний полюсов оси вращения Земли и ее главной полярной оси инерции.
Сезонные перераспределения воздушных атмосферных масс, изменения уровня грунтовых вод, изменения снеговой нагрузки и др. процессы, происходят в тонкой сферической оболочке, охватывающей поверхность Земли. Эти фактически распределенные по поверхности Земли переменные массы (изменяющиеся с годовым периодом) приводят к годовому смещению центра масс Земли. А вследствие их ньютоновского притяжения возникают периодические вынуждающие силы, действующие на все оболочки Земли и в частности на ее твердое ядро. Указанные силы, безусловно, приводят к соответствующим динамическим эффектам.
Основные концентрации воздушных и снеговых масс происходят в Сибири зимой. Именно этим объясняют, в основном, годовые вариации в движении полюса Земли и в ее суточном вращении [10]. Естественно предположить, что сезонное смещение центра масс Земли характеризуется основной составляющей, тяготеющей к направлению геоцентр-условный центр Сибири. Причем наибольшее смещение в северное полушарие должно быть именно зимой .
Именно такое смещение геоцентра было найдено в недавней работе Montag and et.al. (1995) на основе данных наблюдений спутников Lageos 1,2 и по данным GPS [11].
Сезонную вариацию обнаруживают все три координаты геоцентра (в гринвичской системе координат Oxyz данной эпохи). Соответствующие амплитуды этих смещений составляют
Используя данные (37), годовому смещению геоцентра сопоставим
условное периодическое прямолинейное движение вдоль оси O![]() ,
направленной из точки О к точке на поверхности Земли с географическими
координатами 66.9o с.ш., 41.9o в.д. с периодом год
и амплитудой А=19.89 мм.
,
направленной из точки О к точке на поверхности Земли с географическими
координатами 66.9o с.ш., 41.9o в.д. с периодом год
и амплитудой А=19.89 мм.
В аналитической форме указанное смещение можно представить
так: ![]() (38 )
(38 )
где ![]() -
частота сезонных изменений, t - время, отсчитываемое от начала года,
-
частота сезонных изменений, t - время, отсчитываемое от начала года, ![]() -
начальная фаза (в соответствии с [11]
-
начальная фаза (в соответствии с [11] ![]() ).
).
Смещение (38) можно рассматривать как вызываемое двумя
фиктивными гармоническими массами ![]() расположенными при полюсах оси O
расположенными при полюсах оси O![]() на поверхности Земли, причем
на поверхности Земли, причем ![]()
Опираясь на приведенные данные о движении геоцентра,
определим составляющие силы ![]() ньютоновского
притяжения со стороны сезонно-изменяемых приповерхностных масс.
ньютоновского
притяжения со стороны сезонно-изменяемых приповерхностных масс.
Сезонное отклонение в нагрузке на поверхность в точке
с географическими координатами ![]() ,
, ![]() (
(![]() - дополнение
до широты) определяется интегралом [10]:
- дополнение
до широты) определяется интегралом [10]: ![]() где
где ![]() и
и ![]() - средняя и текущая плотность в точке со сферическими координатами r,
- средняя и текущая плотность в точке со сферическими координатами r, ![]() ,
, ![]() (в
гринвичской системе координат Oxyz).
(в
гринвичской системе координат Oxyz).
Положение центра масс Земли в системе координат Oxyz (данной эпохи) определяется радиус-вектором
Если пренебречь малыми смещениями внутреннего ядра Земли
, то для вектора силы притяжения со стороны приповерхностных изменяемых
масс Земли ![]() получим формулу,
аналогичную (39) :
получим формулу,
аналогичную (39) :
Из формул (39) и (40) следуют простые соотношения:
Вынужденное колебание ядра определяется как частное решение дифференциального уравнения (42):
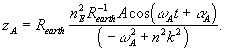
Т.к. ![]() то
приближено
то
приближено
Для рассматриваемых в данной работе моделей взаимодействия
жидкого и твердого ядра Земли (см. п. 2.1) численные значения амплитуды
(43) составляют: а)![]() ,
е)
,
е)![]() ,
p)
,
p)![]() .
.
Покажем, что все процессы медленного перераспределения масс Земли приводят к вековому смещению центра масс твердого ядра. К этим процессам, в первую очередь, мы отнесем: изменение уровня Мирового океана, таяние ледников, изменения ледовых покровов Антарктиды и Гренландии, а также процессы аккумуляции масс вследствие субдукции океанических плит [12], [13].
Все указанные процессы приводят к медленному перераспределению масс во внешней оболочке Земли, в результате которого происходит концентрация масс для одних областей и их убывание для других. И в общем случае сила притяжения, действующая со стороны этих масс на твердое ядро вековым образом меняется во времени.
Рассмотрим сначала общие свойства векового движения твердого ядра, а затем проанализируем и оценим возможную роль упомянутых выше геофизических и тектонических процессов.
Предположим, что вследствие медленной перестройки динамического
строения Земли ее центр масс совершает вековое движение из положения в
данную эпоху со скоростью ![]() ,
постоянные проекции которой на оси системы координат Oxyz обозначим
,
постоянные проекции которой на оси системы координат Oxyz обозначим ![]() .
Предположим, что это смещение геоцентра вызвано вековыми движениями приповерхностных
масс, т.е. происходящих в тонкой сферической оболочке со средним радиусом,
равным среднему радиусу Земли
.
Предположим, что это смещение геоцентра вызвано вековыми движениями приповерхностных
масс, т.е. происходящих в тонкой сферической оболочке со средним радиусом,
равным среднему радиусу Земли ![]() см.
Тогда, фактически повторяя рассуждения п. 7 , для компонент силы притяжения
этих перестраиваемых масс, действующей на твердое ядро, получим выражения,
аналогичные (41):
см.
Тогда, фактически повторяя рассуждения п. 7 , для компонент силы притяжения
этих перестраиваемых масс, действующей на твердое ядро, получим выражения,
аналогичные (41):
На основе общих уравнений движения из п.3 получаем уравнения движения твердого ядра под действием силы (44):
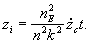 (46)
(46)Отметим основные свойства этого движения:
1) скорость векового движения твердого ядра по величине равна
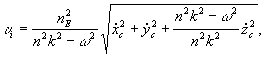
2) векторы скоростей ![]() и
и ![]() центров
масс Земли и внутреннего ядра являются компланарными и расположены в меридиональной
плоскости гринвичской системы координат, а их продолжения пересекают плоскость
Oxy в точке О и в точке
центров
масс Земли и внутреннего ядра являются компланарными и расположены в меридиональной
плоскости гринвичской системы координат, а их продолжения пересекают плоскость
Oxy в точке О и в точке ![]() ,
отстоящей от начала координат на расстоянии
,
отстоящей от начала координат на расстоянии ![]()
3) траектории вековых движений центров масс Земли и внутреннего
ядра расположены в указанной меридиональной плоскости и образуют друг с
другом угол ![]() ,
для которого
,
для которого
Описанные эффекты получены на основе упрощенных уравнений движения и имеют смысл лишь при движениях в малой окрестности центра Земли.
Таким образом, располагая той или иной информацией о движении геоцентра, по формулам (46) можно сразу найти скорость векового движения внутреннего ядра по величине и направлению.
В качестве иллюстрации изучим влияние на движение внутреннего ядра притяжения масс, вековым образом перераспределяющихся вблизи поверхности Земли при изменении уровня Мирового океана, ледовых покровов Гренландии и Антарктиды, а также вследствие субдукции океанических плит.
В соответствии с данными [12] примем, что уровень Мирового
океана возрастает со скоростью ![]() мм/год,
а нарастание ледовых покровов Гренландии и Антарктиды происходит со скоростью
мм/год,
а нарастание ледовых покровов Гренландии и Антарктиды происходит со скоростью ![]() мм/год
и
мм/год
и ![]() мм/год,
соответственно.
мм/год,
соответственно.
Конечно, значительные погрешности в значениях указанных характеристик не позволяют говорить о реальном соотношении массообмена лед-вода, но эти значения позволили сделать некоторые предварительные оценки параметров смещения геоцентра [15] и позволяют оценить параметры векового движения центра масс внутреннего ядра.
На положение геоцентра могут оказывать существенное влияние массы океанических плит, аккумулируемые в окрестностях зон субдукции. Именно этот механизм позволил полностью объяснить наблюдаемое вековое движение полюса оси вращения Земли [13],[14].
По значениям скоростей ![]() из
работ [14] - [16] с помощью формул (46) для указанных выше механизмов были
найдены аналогичные составляющие (в гринвичской системе координат Oxyz)
для скорости движения центра масс внутреннего ядра Земли
из
работ [14] - [16] с помощью формул (46) для указанных выше механизмов были
найдены аналогичные составляющие (в гринвичской системе координат Oxyz)
для скорости движения центра масс внутреннего ядра Земли ![]() .
Так для модели e) (п.2.1) указанные вариации составляют :
.
Так для модели e) (п.2.1) указанные вариации составляют :
вследствие изменения уровня мирового океана
![]() = -11.5 ± 3.8 см/век,
= -11.5 ± 3.8 см/век, ![]() =
-11.6 ± 3.8 см/век,
=
-11.6 ± 3.8 см/век, ![]() =
-13.0 ± 4.3 см/век;
=
-13.0 ± 4.3 см/век;
вследствие изменения ледового покрова Гренландии
![]() = 3.6 ± 14.2 см/век,
= 3.6 ± 14.2 см/век, ![]() =
-3.0 ± 12.0 см/век,
=
-3.0 ± 12.0 см/век, ![]() =
13.6 ± 54.3 см/век;
=
13.6 ± 54.3 см/век;
вследствие изменения ледового покрова Антарктиды
![]() = -2.1 ± 2.1 см/век,
= -2.1 ± 2.1 см/век, ![]() =
5.1 ± 5.1 см/век,
=
5.1 ± 5.1 см/век, ![]() =-77.0
± 77.0 см/век;
=-77.0
± 77.0 см/век;
вследствие притяжения аккумулируемых при субдукции масс плит
![]() = -73.1 см/век ,
= -73.1 см/век , ![]() =
18.8 см/век ,
=
18.8 см/век , ![]() =
16.7 см/век .
=
16.7 см/век .
Выявленные вековые эффекты в движении твердого ядра, вообще говоря, приводят к существенным изменениям его положения на геологических интервалах времени.
Автор выражает благодарность Н.А.Чуйковой за поддержку данной работы и полезные дискуссии.
Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований, грант 94-05-16784 и грант 96-05-65015.