

ГРАВИТАЦИОННОЕ ПОЛЕ МАРСА
  ГРАВИТАЦИОННОЕ ПОЛЕ МАРСА |
|---|
Разложение гравитационного потенциала планеты по сферическим гармоникам имеет вид
,
где Gm0 - произведение гравитационной постоянной на массу Марса,
R0 - экваториальный радиус Марса,
r ,
φ , λ - радиус-вектор, широта и долгота частицы в ареоцентрической экваториальной
системе координат,
Pnk - присоединенные функции Лежандра (
при k > 0 ),
Pn - полиномы Лежандра ( при k = 0
),
Cnk , Snk - коэффициенты тессеральных гармоник
разложения потенциала,
Jn = - Cn0 - коэффициенты
зональных гармоник разложения потенциала.
Исходные значения постоянных следующие:
Gm0 = 42828.4 км3/с2,
R0 = 3394
км.
В таблице приведены
нормализованные коэффициенты потенциала Марса. Связь между нормализованными и
ненормализованными коэффициентами задается следующей формулой
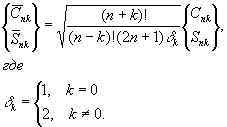
ГРАВИТАЦИОННОЕ ПОЛЕ МАРСА (12 степени и порядка)
| n | k | Ĉnk |
Ŝnk |
n | k | Ĉnk | Ŝnk |
|---|---|---|---|---|---|---|---|
| 2 | 0 |
-876.10004 |
6 | 4 | 2.11695 | 1.29677 | |
| 3 | 0 | -11.17932 | 7 | 4 | 2.57337 | 0.60075 | |
| 4 | 0 | 3.39646 | 8 | 4 | -0.56278 | 3.04243 | |
| 5 | 0 | 11.94782 | 9 | 4 | -1.82713 | -1.82521 | |
| 6 | 0 | 0.95118 | 10 | 4 | -2.17118 | -1.10625 | |
| 7 | 0 | -0.64397 | 11 | 4 | -1.74195 | 0.86302 | |
| 8 | 0 | -0.07718 | 12 | 4 | -3.15088 | 0.95681 | |
| 9 | 0 | -2.35474 | 5 | 5 | -4.19976 | 2.68363 | |
| 10 | 0 | -1.69819 | 6 | 5 | 1.19957 | 2.88149 | |
| 11 | 0 | -1.32526 | 7 | 5 | 0.87602 | -1.82104 | |
| 12 | 0 | -0.75032 | 8 | 5 | -7.67396 | -1.48639 | |
| 3 | 1 | 4.53923 | 24.27684 | 9 | 5 | 5.64058 | -4.04659 |
| 4 | 1 | 2.79383 | 4.96864 | 10 | 5 | -2.12520 | 3.86293 |
| 5 | 1 | 1.50057 | 4.39836 | 11 | 5 | -0.89633 | -2.40769 |
| 6 | 1 | 5.06255 | -5.06255 | 12 | 5 | 4.05614 | 2.98713 |
| 7 | 1 | -4.68089 | 5.71551 | 6 | 6 | 3.84012 | 1.53931 |
| 8 | 1 | 3.17404 | -6.68414 | 7 | 6 | -1.05321 | -3.23803 |
| 9 | 1 | -0.00391 | 0.00145 | 8 | 6 | -1.19139 | -0.58019 |
| 10 | 1 | -2.53042 | 3.66725 | 9 | 6 | 2.29895 | -3.03875 |
| 11 | 1 | -0.43072 | -3.17273 | 10 | 6 | 0.15382 | 3.27933 |
| 12 | 1 | 1.79823 | -1.81442 | 11 | 6 | -1.52224 | -1.31630 |
| 2 | 2 | 85.08972 | 48.48551 | 12 | 6 | 0.66204 | -3.39938 |
| 3 | 2 | -17.17102 | 9.05034 | 7 | 7 | 0.37316 | -3.20110 |
| 4 | 2 | -1.55370 | -9.81689 | 8 | 7 | -1.92550 | 2.61934 |
| 5 | 2 | -3.63391 | -1.79627 | 9 | 7 | 1.83141 | 1.70025 |
| 6 | 2 | 2.90876 | 1.72510 | 10 | 7 | -2.56323 | -0.53173 |
| 7 | 2 | 1.35831 | 2.53353 | 11 | 7 | 5.97213 | -0.16338 |
| 8 | 2 | 3.91598 | -1.75760 | 12 | 7 | -1.99983 | 2.73047 |
| 9 | 2 | 5.46435 | -0.96986 | 8 | 8 | -1.18752 | -0.55463 |
| 10 | 2 | 1.49405 | 3.20310 | 9 | 8 | 1.52922 | 1.67698 |
| 11 | 2 | 0.75626 | 1.49371 | 10 | 8 | 1.91090 | -0.30612 |
| 12 | 2 | 1.71470 | -0.94399 | 11 | 8 | 0.53943 | 4.19394 |
| 3 | 3 | 34.90951 | 25.60092 | 12 | 8 | 0.11698 | -0.82392 |
| 4 | 3 | 5.98673 | 1.33496 | 9 | 9 | -2.40589 | 0.51106 |
| 5 | 3 | 4.44513 | 2.55021 | 10 | 9 | -2.90963 | -3.69136 |
| 6 | 3 | -0.12124 | -0.39408 | 11 | 9 | -3.44076 | 0.46914 |
| 7 | 3 | 4.43077 | 4.46684 | 12 | 9 | 0.99384 | -0.68860 |
| 8 | 3 | -4.12814 | -2.36553 | 10 | 10 | 0.20097 | -0.11902 |
| 9 | 3 | 3.67050 | 1.62755 | 11 | 10 | 0.18630 | 0.91055 |
| 10 | 3 | -1.66385 | 0.77579 | 12 | 10 | 2.53626 | 1.32534 |
| 11 | 3 | 1.47778 | -4.17005 | 11 | 11 | 3.18144 | 2.12870 |
| 12 | 3 | 2.38075 | -0.74525 | 12 | 11 | 3.69804 | -4.53302 |
| 4 | 4 | -0.86685 | -13.47390 | 12 | 12 | 0.46169 | 3.23248 |
| 5 | 4 | -6.11579 | -2.08040 |