Гравитационное поле Амальтеи
[1] Гравитационное поле Амальтеи
[1]
Некоторые общие сведения
Инерциальные характеристики Амальтеи
Виды Амальтеи
Обобщенные
моменты инерции
Полностью нормализованные стоксовы коэфиициенты
разложения
внешнего гравитационного поля Амальтеи (9 степени и порядка)
Использована топографическая модель Амальтеи [3]. Основные физические и геометрические характеристики вычислены в предположении, что ее плотность постоянна. Для вычисления выбрана гармоническая модель топографии 18 порядка и степени.
Хотя Амальтея имеет очень неправильную форму, динамически она может рассматриваться как почти симметричное тело (В = С). Приводятся Стоксовы коэффициенты до 9 порядка и степени.
| Общие сведения | |||
|
Физическая величина |
Числовое значение |
Размерность | Ссылка |
| Гравитационная постоянная GM | 0.138 | км3/сек2 | |
| Объем */ | (2.44 ± 0.02) × 106 | км3 | [1] |
| Средний радиус r0 **/ | 79.68 | км | [1] |
| Плотность | 1.8 | г/см3 | |
Инерциальные
характеристики Амальтеи,
вычисленные с
использованием топографии и численного интегрирования (величины в скобках)
| Основные моменты инерции ( в единицах Mr02) | ||
A 0.292 (0.283) |
B 0.686 (0.668) |
C 0.705 (0.697) |
Ориентация основных осей (3-2-1 углы Эйлера) |
||
| φ 13.0° (14.0°) |
θ -0.5° (-0.5°) |
ψ
16.5° (19.3°) |
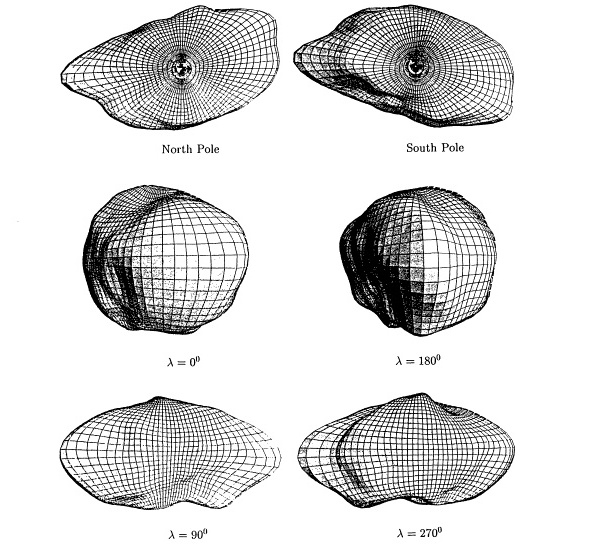
Виды Амальтеи с шести взаимно перпендикулярных направлений, вычисленные на основе гармонического разложения топографии (используется модель 18 порядка и степени). Сверху: виды северного и южного полюсов, экваториальные проекции для долгот 0°, 180°, 90° и 270°.
Обобщенные моменты инерции.
Моменты первого порядка
нормализованы множителем Mr0, моменты второго порядка - множителем Mr02
| Порядок | Численное интегрирование |
Сигма | Из топографии | Отличие в процентах |
| М100 | -0.009 | 0.008 | -0.011 | 8.0 |
| M010 | -0.006 | 0.004 | -0.006 | 2.5 |
| M001 | -0.008 | 0.003 | -0.008 | 3.4 |
| M110 | 0.085 | 0.003 | 0.093 | 9.7 |
| M101 | 0.002 | 0.003 | 0.002 | 3.7 |
| M011 | 0.006 | 0.002 | 0.006 | 3.5 |
| M200 | 0.527 | 0.008 | 0.524 | 0.6 |
| M020 | 0.177 | 0.002 | 0.171 | 3.2 |
| M002 | 0.141 | 0.001 | 0.136 | 3.9 |
Тензор диагональных элементов инерции |
||||
| Ixx | 0.318 | 0.003 | 0.307 | 3.5 |
| Iyy | 0.668 | 0.008 | 0.659 | 1.3 |
| Izz | 0.704 | 0.008 | 0.695 | 1.2 |
Полностью нормализованные стоксовы коэффициенты внешнего гравитационного поля Амальтеи (с коэффициентом 10-2). (Вычислены для радиуса r0 = 79.68 км )
| j | m | Cjm | σC | Sjm | σS |
|---|---|---|---|---|---|
| 1 | 0 | -0.378 | 0.147 | ||
| 1 | 1 | -0.760 | 0.372 | -0.321 | 0.190 |
| 2 | 0 | -9.503 | 0.255 | ||
| 2 | 1 | 0.145 | 0.196 | 0.484 | 0.128 |
| 2 | 2 | 13.665 | 0.451 | 0.676 | 0.353 |
| 3 | 0 | 0.884 | 0.177 | ||
| 3 | 1 | 0.769 | 0.362 | -0.437 | 0.128 |
| 3 | 2 | -1.577 | 0.228 | -0.534 | 0.104 |
| 3 | 3 | -3.527 | 0.481 | 1.420 | 0.312 |
| 4 | 0 | 4.958 | 0.314 | ||
| 4 | 1 | -0.725 | 0.275 | -0.389 | 0.116 |
| 4 | 2 | -6.836 | 0.415 | -2.625 | 0.266 |
| 4 | 3 | 0.532 | 0.224 | 0.599 | 0.194 |
| 4 | 4 | 6.735 | 0.598 | 5.493 | 0.454 |
| 5 | 0 | -0.520 | 0.295 | ||
| 5 | 1 | -1.407 | 0.665 | 0.455 | 0.143 |
| 5 | 2 | 1.084 | 0.335 | 0.245 | 0.168 |
| 5 | 3 | 3.007 | 0.660 | -0.691 | 0.389 |
| 5 | 4 | -1.482 | 0.252 | -1.027 | 0.223 |
| 5 | 5 | -7.109 | 0.961 | -0.425 | 0.564 |
| 6 | 0 | -4.925 | 0.662 | ||
| 6 | 1 | 0.957 | 0.645 | 0.132 | 0.148 |
| 6 | 2 | 6.456 | 0.884 | 2.085 | 0.352 |
| 6 | 3 | -0.706 | 0.560 | -0.348 | 0.296 |
| 6 | 4 | -5.390 | 0.905 | -3.741 | 0.518 |
| 6 | 5 | 0.698 | 0.459 | 0.499 | 0.320 |
| 6 | 6 | 6.143 | 1.298 | 5.427 | 0.793 |
| 7 | 0 | 0.806 | 0.709 | ||
| 7 | 1 | 2.993 | 1.431 | -0.367 | 0.205 |
| 7 | 2 | -1.476 | 0.934 | -0.004 | 0.278 |
| 7 | 3 | -4.429 | 1.422 | 0.568 | 0.544 |
| 7 | 4 | 1.855 | 0.839 | 0.767 | 0.362 |
| 7 | 5 | 6.916 | 1.532 | 0.866 | 0.773 |
| 7 | 6 | -1.732 | 0.800 | -1.798 | 0.356 |
| 7 | 7 | -11.831 | 2.164 | -5.702 | 1.413 |
| 8 | 0 | 6.585 | 1.497 | ||
| 8 | 1 | -1.967 | 1.673 | -0.213 | 0.258 |
| 8 | 2 | -8.628 | 2.035 | -2.603 | 0.656 |
| 8 | 3 | 1.583 | 1.610 | 0.442 | 0.583 |
| 8 | 4 | 7.121 | 2.030 | 4.252 | 1.022 |
| 8 | 5 | -1.259 | 1.451 | -0.397 | 0.739 |
| 8 | 6 | -6.472 | 2.219 | -4.879 | 1.266 |
| 8 | 7 | 1.533 | 1.117 | 0.566 | 0.853 |
| 8 | 8 | 10.190 | 3.255 | 7.363 | 1.975 |
| 9 | 0 | -1.853 | 2.085 | ||
| 9 | 1 | -5.760 | 3.302 | 0.357 | 0.381 |
| 9 | 2 | 2.999 | 2.842 | 0.014 | 0.583 |
| 9 | 3 | 7.554 | 3.284 | -0.309 | 1.038 |
| 9 | 4 | -3.465 | 2.659 | -0.834 | 0.879 |
| 9 | 5 | -10.216 | 3.392 | -1.746 | 1.553 |
| 9 | 6 | 3.107 | 2.488 | 2.113 | 0.931 |
| 9 | 7 | 12.739 | 3.696 | 6.422 | 2.223 |
| 9 | 8 | -1.918 | 2.339 | -3.107 | 0.948 |
| 9 | 9 | -17.161 | 4.819 | -16.809 | 4.147 |
Kr. Gozdziewski, A. Maciejewski, Ph. J. Stooke. A Model of the Gravitational Field of Amalthea. Part I: Derivation. Earth, Moon and Planets. 1994. 64. P. 243-264.
Anderson, J. D.; Anabtawi, A.; Jacobson, R. A.; Johnson, T. V.; Lau, E. L.; Moore, W. B.; Schubert, G.; Taylor, A. H.; Thomas, P. C.; Weinwurm, G. Gravity Field, Topography, and Interior Structure of Amalthea. 2002. American Geophysical Union, Fall Meeting 2002, abstract #P12C-13
Stooke P.J. 1994. The Geology of Amalthea. Earth, Moon and Planets.