НЕБЕСНАЯ МЕХАНИКА
Вопросы к экзамену
1. Общая задача двух тел. Интегралы движения центра масс.
2. Уравнения задачи двух тел в относительных координатах.
3. Интегралы площадей. Интеграл энергии.
4. Интегралы Лапласа.
5. Соотношения между первыми интегралами. Интеграл, явно содержащий время.
6. Траектория движения тела в орбитальной /прямоугольной и полярной/ системе координат. Орбитальные координаты и компоненты скоростей как функции истинной аномалии.
7. Кеплеровские элементы орбиты, их связь с произвольными постоянными общего интеграла.
8. Интегралы площадей в орбитальной, прямоугольной и полярной, системах координат. Интеграл, содержащий явно время.
9. Общее решение уравнений невозмущенного движения.
10. Первый и второй обобщенные законы Кеплера. Типы невозмущенного движения. Определение типа движения по начальным условиям.
11. Вывод уравнений Кеплера.
12.Геометрический смысл истинной, эксцентрической и средней аномалий. Вывод зависимости между истинной и эксцентрической аномалиями.
13. Выражение прямоугольных и полярных орбитальных координат и скоростей через эксцентрическую аномалию.
14.Третий обобщенный закон Кеплера. Определение масс планет, имеющих спутники.
15. Вычисление прямоугольных координат и скоростей в эллиптическом движении/сводка формул/.
16. Гиперболическое движение. Вывод аналога уравнений Кеплера.
17. Геометрический смысл аналога эксцентрической аномалии в гиперболическом движении. Вывод зависимости между истинной и аналогом эксцентрической аномалии в гиперболическом движении.
18. Вычисление прямоугольных координат и скоростей в гиперболическом движении /сводка формул/.
19. Параболическое движение. Уравнение Барнера.
20.Вычисление прямоугольных координат и скоростей в параболическом движении /сводка формул/.
21.Прямолинейное движение. Типы прямолинейного движения.
22. Вычисление невозмущенной эфемериды планет и комет.
23. Определение постоянных интегрирования и кеплеровских элементов орбиш по начальным условиям.
24.Разложение координат эллиптического движения по степеням эксцентриситета.
25. Формула Лагранжа. Ряд Лагранжа. Предел Лапласа.
26. Разложение координат эллиптического движения в ряды Фурье. Теорема Дирихле. Вывод разложения для эксцентрической аномалии. Общий вид разложений для координат.
27. 3адача многих тел. Десять классических интегралов. Не существование других интегралов.
28.Уравнение Лагранжа - Якоби.
29. Оскулирующие элементы. Основная операция.
30. Вывод уравнения для dp/dt.
31. то же для d /dt и dM0/dt.
/dt и dM0/dt.
32. то же для di/dt.
33. то же для de/dt.
34. то же для d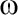 /dt.
/dt.
35. Вывод общего интеграла в задаче двух тел методом Гамильтона - Якоби.
36. Элементы Якоби и их связь с кеплеровскими элементами.
37. Метод вариации произвольных постоянных для канонических систем. Его использование
для вывода уравнений Лагранжа.
38. Вывод уравнений Лагранжа /для большой полуоси/. Для da/dt и d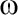 /dt/
/dt/
39. Метод Пуанкаре малого параметра.
40. Классификация возмущений.
41. Теорема Лапласа - Лагранжа о вековых возмущениях первого порядка больших полуосей планет.
42. Теорема Лапласа об устойчивости солнечной-системы. Теорема Арнольда.
43. Ограниченная задача трех тел. Вывод уравнений движения круговой задачи. Интеграл Якоби.
44. Точки либрации в ограниченной задаче трех тел.
45. Поверхности Хилла. Устойчивость по Хиллу.
46. Движение ИСЗ. Не центральность поля тяготения. Влияние атмосферы. Реактивные силы.
47. Влияние сопротивления атмосферы. Парадокс торможения в атмосфере. Время существования ИСЗ.
48. Активные силы. Гомановские перелеты.
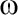 /dt.
/dt.
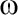 /dt/
/dt/