Необычные свойства быстрого рентгеновского
Барстера.
V.A.Lefebvre, Yu.N.Efremov
POSSIBLE ANALOGUES OF COGNITIVE PROCESSES IN THE PATTERNS OF X--RAY
VARIABILITY OF THE RAPID BURSTER.
http://xxx.lanl.gov/abs/astro-ph/9808057
представлено к публикации в Journal British Interplanetary Society, 1998.
Рентгеновский источник MXB 1730-335 - один из 125 известных
мало массивных рентгеновских двойных звезд. Примерно у 50 из них
вспышки (тип I) связаны с термоядерной активностью на поверхности
нейтронных звезд, что приводит к рентгеновскому излучению. Уникальная
особенность MXB 1730-335, которая послужила причиной его названия
Быстрый Барстер (ББ), состоит в том, что он производит быстрые
повторяющиеся рентгеновские вспышки, имеющие некоторые регулярные
структуры. Активность его носит периодический характер и длится от 2
до 6 недель с интервалами около 6 месяцев. Подобные вспышки (тип II) в
последнее время найдены также и у других рентгеновских звезд (GRO
J1744-28), но у них пока не обнаружено столь сложного поведения, как у
ББ. Авторы обращают внимание на определенные черты сходства рентгеновской
активности ББ с характеристиками активности, изучаемыми в психологии.
Различные вспышки ББ имеют разную длительность, однако профили
их подобны. Если нормировать длительность вспышки по отношению к
интервалу между двумя пиками, то получается инвариантный нормированный
профиль, обладающий следующими свойствами.
- Высота пиков образует двойную геометрическую прогрессию: одна
прогрессия для нечетных пиков и другая для четных пиков с одним и тем
же показателем прогрессии
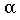 =0.57;
временные интервалы между четными
и нечетными пиками образуют ту же геометрическую прогрессию с тем же
показателем 0.57. =0.57;
временные интервалы между четными
и нечетными пиками образуют ту же геометрическую прогрессию с тем же
показателем 0.57.
- В спектре мощности коротких (менее 25 сек.) вспышек отношение
центральных частот спектральных пиков приблизительно постоянно для всех
вспышек и равно 1.59, что близко к золотому сечению
F=(
 +1)/2=1.618. При этом, если отбросить наблюдения с большой
ошибкой и оставить только наблюдения со средней квадратической ошибкой +1)/2=1.618. При этом, если отбросить наблюдения с большой
ошибкой и оставить только наблюдения со средней квадратической ошибкой
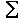 , не превышающей 0.02, то отношение частот увеличивается до 1.61,
то есть согласие с золотым сечением становится более выраженным. , не превышающей 0.02, то отношение частот увеличивается до 1.61,
то есть согласие с золотым сечением становится более выраженным.
Двойная геометрическая прогрессия и золотое сечение появляются
совместно в построенной ранее В.Лефевром формальной модели субъекта,
способного проводить последовательные акты саморефлексии. Было
показано, что эта модель может быть описана с помощью системы
тепловых машин. Температуры резервуаров образуют убывающую
геометрическую прогрессию. Каждая последующая машина берет из горячего
резервуара ровно столько тепла, сколько передала в него предыдущая и
производит работу равную "потерянной" работе предыдущей машины, то
есть разнице между максимальной работой, которую могла бы произвести
эта машина (если бы она была обратимой), и фактически произведенной ею
работой. В такой системе коэффициент полезного действия всех машин с
нечетными номерами равен к.п.д. первой машины, а коэффициент полезного
действия всех машин с четными номерами равен к.п.д. второй машины.
То есть к.п.д. машин формирует дополнительный ряд x1,
x2, x1, x2 ...
Работа, произведенная этими машинами образует двойную
геометрическую прогрессию:
с нечетными номерами (n=2k+1): W2k+1=W1(T2/T1)k,
с четными номерами (n=2k+2): W2k+2=W2(T2/T1)k,
где T1 и T2 - температуры 1-ого и 2-го резервуаров соответственно и
k=0,1,2,3, ...
В рамках психологической модели рефлексии машина 1 есть
теоретический аналог субъекта S1, машина 2 - аналог отображения себя
субъектом S1 или "образ себя" (S2) у субъекта
S1. Последующие
машины представляют иерархию отображений себя S3, S4,
..., Sn,
являющуюся результатом последовательных актов саморефлексии.
Аналогом чувств в этой модели являются мощности машин. Работа W1,
произведенная машиной 1, соответствует интенсивности чувства, которое
испытывает субъект S1. Работа, произведенная последующими машинами,
соответствует иерархии осознаваемых образов этого чувства: W2 -
соответствует тому чувству (той интенсивности испытываемого чувства),
которое субъект "видит" (или осознает) в себе; W3 - соответствует
чувству, которое "видит" не сам субъект, а его "образ себя" и т.д.
Величина x1 соответствует стимулу активности субъекта, т.е.
воздействию, с которым окружающая среда (мир) вынуждает его сделать
тот или иной выбор, а x2 - познавательный образ этого стимула, или
представление субъекта о том, с какой силой мир диктует ему сделать
этот выбор. В тех случаях, когда отсутствуют объективные критерии
выбора, x1 = 1/2, x2 = 1/F = 0.618 ...
Субъект в этом случае не
выбирает случайно между двумя альтернативами, что должно было бы
приводить к равным вероятностям выбора альтернатив, а выбирает
согласно правилу золотого сечения: одна из альтернатив выбирается с
вероятностью 0.618, а другая - с вероятностью 1 - 0.618 = 0.382.
Этот вывод модели подтверждается психологическими экспериментами и
позволяет объяснить ассиметрию человеческого выбора.
Активность ББ может быть интерпретирована в рамках рассмотренной
модели субъекта как аналог познавательных процессов рефлексии.
Последовательность пиков ставится в соответствие с рядом
машин, первая машина соответствует первому пику, вторая -
второму пику и т.д. Последовательность высот пиков h1,
h2, h3 ...
соответствует ряду величин работы W1, W2,
W3 ..., проделанной этими
машинами. Связь между последовательностью машин и параметрами
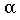 и и
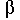 дается уравнением
T2/T1=
дается уравнением
T2/T1=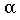 и W1/W2=
и W1/W2=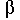 . Отношение между
W1, W2 и W3 пропорционально величинам:
x1, (1-x1)x2, (1-x1)(1-x2)x1.
Величины x1 и x2 связаны с . Отношение между
W1, W2 и W3 пропорционально величинам:
x1, (1-x1)x2, (1-x1)(1-x2)x1.
Величины x1 и x2 связаны с
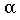 и и
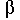 следующей системой уравнений:
следующей системой уравнений:
(1-x1)(1-x2)=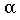 , ,
[(1-x1)x2]/x1=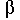
В наблюдениях 1983 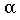 =0.57, =0.57,
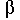 =0.81. Решая систему
уравнений (1),
получаем x1=0.238 и x2=0.252. В наблюдениях 1984 =0.81. Решая систему
уравнений (1),
получаем x1=0.238 и x2=0.252. В наблюдениях 1984
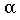 =0.57, =0.57,
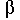 =0.77,
x1=0.243 и x2=0.247. Эти данные могут быть
интерпретированы как доказательство того, что в наблюдательный период
1983-84 гг., величины x1 и x2 оцениваются как 0.25.
При x1=x2=0.25
точные величины наблюдаемых параметров =0.77,
x1=0.243 и x2=0.247. Эти данные могут быть
интерпретированы как доказательство того, что в наблюдательный период
1983-84 гг., величины x1 и x2 оцениваются как 0.25.
При x1=x2=0.25
точные величины наблюдаемых параметров
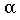 =(9/16)=0.5625 и =(9/16)=0.5625 и
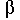 =(3/4)=0.75.
Для x1=x2 двойная геометрическая прогрессия
обращается в регулярную с общим отношением =(3/4)=0.75.
Для x1=x2 двойная геометрическая прогрессия
обращается в регулярную с общим отношением
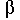 (в этом случае (в этом случае
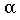 = =
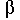 2).
Равенство коэффициентов машин с нечетными и четными номерами
предполагает важную интерпретацию в рассматриваемой модели, а именно:
субъект, который моделируется с помощью такого ряда машин имеет
правильную саморефлексию. 2).
Равенство коэффициентов машин с нечетными и четными номерами
предполагает важную интерпретацию в рассматриваемой модели, а именно:
субъект, который моделируется с помощью такого ряда машин имеет
правильную саморефлексию.
Обсуждается, что может означать связь между высотами пиков и
величиной работы, произведенной системой тепловых машин. Возможны два
варианта:
- пики генерируются непосредственно некоторым физическим
процессом, который работает аналогично цепи тепловых машин;
- форма профиля есть специальный сигнал, содержащий информацию о
познавательном процессе связанном как с двойной геометрической
прогрессией, так и с золотым сечением. Во втором случае физический
механизм, генерирующий наблюдаемый профиль вспышки может быть
существенно различным. Второй вариант представляется более вероятным,
так как высоты пиков напрямую не связаны с энергией, излучаемой ББ,
поскольку рассматривается некий осредненный нормированный профиль
вспышки.
Подобие параметров некоторых процессов, проявляющихся в ББ, с
определенными явлениями изучаемыми познавательной психологией,
указывает на возможность внутренней схожести между активностью ББ и
человеческой познавательной способностью.
Каждый новый сет наблюдений ББ обнаруживает новые загадочные
особенности. Например, Dottani и др. нашли 5-ти герцовые
квазипериодические колебания у вспышек II типа, которые очень сильны в
течение начального пика, отсутствуют во втором пике и снова сильны в
третьем пике. Эти колебания могут быть описаны как периодические с
периодом изменяющимся до 25% в течении вспышки; изменения периода
также периодические. Колебания как бы "знают", какая у них частота.
Как заметил Kawai, и временной инвариант профилей вспышек II типа так же
показывает, что в начале вспышки "система знает, как долго вспышка
собирается продолжаться". Аналогичные явления свойственны человеческой
познавательной деятельности, как, например, в спонтанной речи: начало
данной структуры предложения зависит от финальной структуры этого
предложения, взятого как целое.
ББ расположен в шаровом скоплении Liller 1 на расстоянии около 10
кпс от Солнца. Учитывая некоторую неопределенность в определении
расстояния до скопления, он может находиться значительно ближе к
центру Галактики. В любом случае местонахождение ББ в шаровом
скоплении указывает, что его возраст около 15 млрд. лет.
Недавно обнаружен радиоисточник вблизи ББ.
Поведение радиоисточника (вкл/выкл) коррелировано с соответствующим поведением
(вкл/выкл) рентгеновского излучения с вероятностью случайного
совпадения 1.6%. Авторы отмечают, что координаты радиоисточника точно
совпадают с центром скопления, а ББ сдвинут от него на 8 секунд, что составляет
4-5.6 среднеквадратической ошибки определения положения источника.
Это делает ситуацию даже более привлекательной с точки зрения гипотезы
артефакта.
|
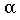 =0.57;
временные интервалы между четными
и нечетными пиками образуют ту же геометрическую прогрессию с тем же
показателем 0.57.
=0.57;
временные интервалы между четными
и нечетными пиками образуют ту же геометрическую прогрессию с тем же
показателем 0.57.
 +1)/2=1.618
+1)/2=1.618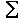 , не превышающей 0.02, то отношение частот увеличивается до 1.61,
то есть согласие с золотым сечением становится более выраженным.
, не превышающей 0.02, то отношение частот увеличивается до 1.61,
то есть согласие с золотым сечением становится более выраженным.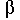 дается уравнением
T2/T1=
дается уравнением
T2/T1=